Движение заряженных частиц в магнитном поле

При заданных полях и 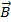задача о движении заряженной частицы – это обычная задача клас­си­ческой механики о движении под действием известных сил. В однородных электри­чес­ком и магнитном полях движение заряженной частицы про­исходит достаточно просто и может быть изучено элементарными методами.

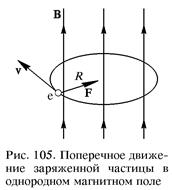
Движение заряженной частицы в однородном магнитном поле под действием силы Лоренца происходит следующим образом. В плоскости, перпендикулярной индукции магнитного поля, частица равномерно обращается по окружности со скоростью υ (рис. 105). Ра­диус R этой окружности пропорционален перпендикулярной магнитному полю составляющей скорости части­цы υ _^, а частота обращения частицы ω _с от скорости не зависит и равна произведению удельного заряда частицы на индукцию магнитного поля. Если при этом частица имеет еще и составляющую скорости υ _|| вдоль магнитного поля 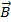, то на такое вра­щение накладывается равномерное движе­ние вдоль поля, так что траектория резуль­тирующего движения представляет собой винтовую линию (рис. 106). Покажем это.

Составляющая скорости частицы вдоль магнитного поля υ _|| и не меняется при движе­нии. Cо­ста­вляющая скорости, перпендику­лярная магнитному полю, υ _^меняется только по напра­вле­нию, так как действующая сила перпендикулярна скорости, поэтому в проекции на плоско­сть, перпендикулярную магнитному полю, движение частицы проис­ходит по окружности неко­то­рого радиуса R с центростремительным ускорением , обусловленным силой Лоренца. Записывая выражение для этой силы в виде qυ _^ В и приравнивая ее в соответствии со вто­рым законом Ньютона произведению массы на ускорение, имеем

откуда

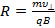(16)

Частота обращения частицы ω _с = 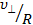, как видно из (16), равна:

(17)

Независимость частоты обращения частицы в магнитном поле от ее скорости и от радиуса круговой орбиты (а тем самым и от энергии) лежит в основе принципа действия циклотрона исторически первого и наиболее простого из циклических ускорите­лей заряженных частиц, широко применяемого и в наши дни в самых различных областях науки и техники. От названия этого прибора происходит термин «циклотронная частота» для частоты обращения заряженной частицы в магнитном поле, даваемой формулой (17). Отклонение заряженных частиц поперечным магнитным полем используется также в масс-спектрометрах — приборах для точных измерений масс атомов и молекул, в установках для электро­магнитного разделения изотопов. В телевизионных трубках с по­мощью магнитного поля производится строчная и кадровая развер­тка электронного луча по экрану.