
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Сила Ампера
|
|
Рассмотрим сначала силу, действующую на проводник с током, находящийся в магнитном поле – силу Ампера. Ее существование можно продемонстрировать простым опытом, схема которого показана на рис. 100. Направление силы Ампера соответствует правилу левой руки: когда магнитные силовые линии входят в ладонь, а четыре выпрямленных пальца указывают направление тока, отставленный в сторону большой палец указывает направление силы. Именно на использовании этой силы основано действие электроизмерительных приборов магнитоэлектрической системы.

Сила Ампера тем больше, чем больше сила тока в проводнике и чем больше индукция магнитного поля. Выражение для этой силы можно получить с помощью формулы (2) § 1, определяющей индукцию магнитного поля через максимальное значение вращающего момента, действующего на рамку с током в однородном магнитномполе. Этот момент обусловлен действующими на стороны рамки силами Ампера. Когда рамка расположена так, как показано на рис. 101 (т. е. магнитные силовые линии параллельны ее плоскости), силы действуют только на ее вертикальные стороны, так как горизонтальные стороны направлены вдоль силовых линий.
Силы Ампера  , действующие на вертикальные стороны рамки, одинаковы и направлены в противоположные стороны, т. е. образуют пару, момент которой равен произведению одной из них на плечо b:
, действующие на вертикальные стороны рамки, одинаковы и направлены в противоположные стороны, т. е. образуют пару, момент которой равен произведению одной из них на плечо b:
М=FАb. (1)
При указанной ориентации рамки этот момент сил максимален и в соответствии с формулой (2) § 1 равен
М=ВIS = ВIlb. 2)
Приравнивая правые части (1) и (2), получаем выражение для силы Ампера, действующей на проводник длиной / с током, расположенный перпендикулярно силовым линиям магнитного поля с индукцией В:
FА = IВl. (3)
Эта формула записана в СИ, где сила тока измеряется в амперах, индукция магнитного поля – в тесла, длина – в метрах. Значение силы получается в ньютонах.
Если проводник с током расположен под углом а к вектору В, то вклад в силу Ампера дает только составляющая магнитного поля, перпендикулярная проводнику. В этом случае выражение для силы Ампера записывается в виде
 (4)
(4)
Выражение для вектора 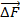 силы, действующей на элемент Δ l проводника, можно записать, используя векторное произведение:
силы, действующей на элемент Δ l проводника, можно записать, используя векторное произведение:
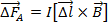 (5)
(5)
Зная силу 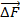 , действующую на отдельный элемент проводника с током, можно найти силу, действующую на весь проводник.
, действующую на отдельный элемент проводника с током, можно найти силу, действующую на весь проводник.
Взаимодействие двух параллельных токов. В качестве примера рассмотрим силу взаимодействия двух бесконечных параллельных проводников, по которым идут токи I1 и I2 (рис. 102). Будем искать силу, действующую на проводник 1в магнитном поле, создаваемом проводником 2. Индукция этого магнитного поля выражается формулой (6) § 1, в которую в качестве I следует подставить ток I2 в проводнике 2, а в качестве r – расстояние d между проводниками:

 (6)
(6)
Кольцевые магнитные силовые линии этого поля перпендикулярны проводнику 1, поэтому в соответствии с формулой (3) действующая на его участок длиной l сила Ампера равна
 (7)
(7)
Если рассмотреть силу, действующую на проводник 2 в магнитном поле, создаваемом проводником 1, то получится тот же самый результат (7).
Рассмотрим с точки зрения полученной формулы опыт Ампера. Видно, что сила взамодействия двух проводников с током пропорциональна как силам тока в них, так и длине взаимодействующей части. Известно, что четвертая основная единица Международной системы единиц – ампер – определяется через магнитное взаимодействие токов. Для этого используют закон взаимодействия двух параллельных токов (7). По определению ампер – это сила неизменяющегося тока, который, проходя по двум прямым параллельным проводникам бесконечной длины и ничтожно малого поперечного сечения, расположенным в вакууме на расстоянии 1 м один от другого, создал бы между этими проводниками силу, равную 2·10–7 Н на каждый метр длины. Подставим в формулу (7) условия опыта для введения новой единицы, чтобы получить значение константы μ о:
 Þ
Þ 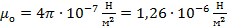 .
.