Относительная линейная независимость

Определение. Векторы называются линейно независимыми относительно подпространства N, если из того, что их линейная комбинация принадлежит подпространству, следует, что все коэффициенты линейной комбинации равны нулю, т.е.

.

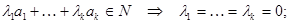
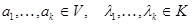Линейная независимость относительно нулевого подпространства совпадает с обычной линейной независимостью. Векторы, линейно независимые относительно подпространства, линейно независимы. Обратное выполняется не всегда.

Теорема. Векторы линейного пространства V/K линейно независимы относительно подпространства N тогда и только тогда, когда их объединение с базисом подпространства образует линейно независимую систему.

Доказательство. Þ Предположим, что векторы 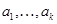линейного пространства V/K линейно независимы относительно подпространства N, 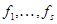– базис N/K и

.

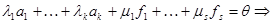
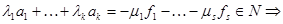
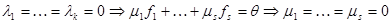Система 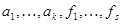линейно независима.

Ü Пусть векторы 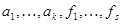линейно независимы в линейном пространстве V/K, где 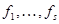– базис пространства N, и пусть 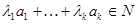. Тогда

.

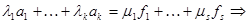
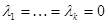Итак, как только 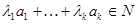, так сразу 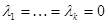. Это означает, что система 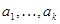линейно независима относительно подпространства. ■