Корневое подпространство

Определение. Подпространство линейного пространства называется инвариантным относительно линейного оператора j, если линейный оператор j элементы подпространства отображает в элементы этого же подпространства.

Теорема. Множество всех корневых векторов линейного пространства V/K, принадлежащих одному собственному значению линейного оператора j, образует подпространство линейного пространства V, инвариантное относительно линейного оператора j.

Доказательство. Для доказательства первой части теоремы достаточно проверить все аксиомы линейного пространства.

Если (j - re) ^hc = q, то (j - re) ^h (j с) = j((j - re) ^hc) = j(q) = q, т.е. если с – корневой вектор, то и j с – тоже корневой вектор, принадлежащий тому же собственному значению. ■

Обозначим через 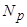множество всех корневых векторов линейного пространства V/K, принадлежащих собственному значению r линейного оператора j. 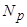– корневоеподпространство, принадлежащее собственному значению r линейного оператора j.

Теорема. Пусть r₁,..., r _m – все попарно различные собственные значения линейного оператора j, действующего в линейном пространстве V/K Тогда линейное пространство V есть прямая сумма корневых подпространств:

V = 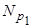Å... Å 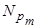(2)

Доказательство. Так как r₁,..., r _m – все различные собственные значения линейного оператора j, то его характеристический многочлен имеет вид:

c(х) = (х - r₁) 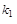... (x - r _m)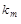

и многочлены

y₁(х) = (x - r₂) 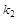(x - r₃) 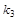... (x - r _m) ,

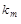y₂(х) = (x - r₁) 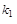(x - r₃) 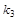... (x - r _m) ,

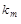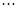
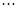
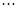
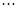
y _m (х) = (x - r₁) 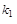(x - r _m -₂) 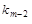(x - r _m)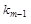

взаимно простые. По теореме о линейном представлении НОД существуют многочлены v ₁(x),..., v_m (x) из K[ x ], для которых

y₁(x) v ₁(x) +... + y _m (x)v _m (x) = 1 или y₁(j) v ₁(j) +... +y _m (j)v _m (j) = e.

Для любого элемента a из линейного пространства V получим

y₁(j) v ₁(j) a + 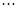+ y _m (j) v_m (j) a = a.

Введем обозначения:

y₁(j) v ₁(j) a = a ₁, 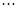, y _m (j) v_m (j) a = a_m.

Тогда a = a ₁ +... +a_m. Так как (j - r _i) 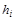y _i (j) = c(j), а по теореме Гамильтона-Кэли линейный оператор c(j) – нулевой, то

(j - r _i e) 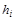a_i = q,

т.е. 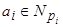, 1 £ i £ m Þ V Í 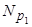+... + 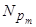Þ

Þ V = +... + .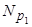

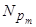Предположим, что y ₁ +... +y_m = q, y_i Î 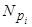, 1 £ i £ m. Тогда у ₁= q,..., y_m = q.В противном случае получаем противоречие с тем, что ненулевые векторы y ₁, 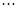, y_m линейно независимы. Из единственности представления нулевого вектора в виде суммы элементов из подпространств следует, что сумма прямая. ■

Замечание. Из доказательства следует, что если

c(х) = (х - r₁) 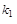... (x - r _m) ,

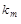то

V = Ker(j -r₁e) 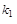Å Ker(j -r₂e) 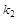Å 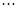Å Ker(j -r _m e) .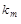