
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Доказательство. Пустьl1ya1 + + ls yas Î Mi –2 Þ
|
|
Пустьl1y a 1 +...+ l s y as Î M i –2 Þ
Þ y(l1 a 1 +...+ l s as) Î M i –2 Þ y i -2y(l1 a 1 +...+ l s as) = q Þ
Þ l1 a 1 +...+ l s as Î M i –1 Þ l1 = 0,..., l s = 0.
Векторы y a 1,..., y as линейно независимы в Mi -1 относительно Mi –2. ■
Перейдем к построению канонического базиса в N r.
Пусть 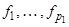 – базис Mk = Nr относительно Mk -1. Тогда элементы
– базис Mk = Nr относительно Mk -1. Тогда элементы 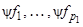 линейно независимы в Mk -1 относительно Mk –2.
линейно независимы в Mk -1 относительно Mk –2.
Дополним систему этих векторов до базиса Mk -1 относительно Mk – 2:
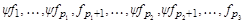 – базис Mk –1 относительно Mk –2.
– базис Mk –1 относительно Mk –2.
Применяя к этим векторам линейный оператор j, получим систему, линейно независимую в Mk –2относительно Mk -3. Вновь дополним ее до базиса Mk -2 относительно Mk –3.
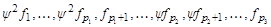
Продолжив действия по описанному алгоритму, получим базис Nr.
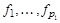
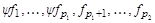
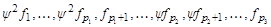 y2
y2
¼........................
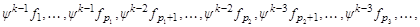
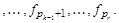
Векторы базиса выписаны в виде таблицы, в которой pk столбцов. Векторы столбца i порождают циклическое подпространство Qi, причем
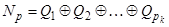 ,
,
где базис подпространства Qi канонический. Следовательно, выписав в строчку столбец за столбцом, получим канонический базис линейного пространства V.
Заметим, что матрица линейного оператора jв этом базисе диагональна тогда и только тогда, когда Nr = M 1.
Пример. Матрица линейного оператора jв базисе e 1, e 2, e 3, e 4, e 5линейного пространства имеет вид
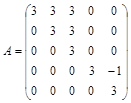 .
.
Построить канонический базис.
Характеристический многочлен c(l) = | А - l Е | линейного оператора имеет один корень l =3.
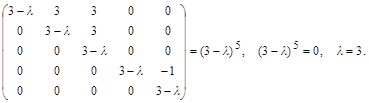
Матрица линейного оператора y = j -3e в этом базисе
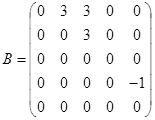 ;
; 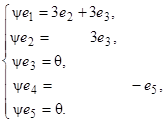
Пусть z =x 1 e 1+... + x 5 e 5, y(z) = q Þ
Þ x 1y e 1 + x 2y e 2 + x 3y e 3 + x 4y e 4 + x 5y e 5= qÞ
Þ x 1(3 e 2+3 e 3) + x 23 e 3 + x 3q + x 4(- e 5) + x 5q = qÞ
Þ 3 x 1 e 2 + 3(x 1 + x 2) e 3 – x 4 e 4 = q.
Эти выкладки в матричном виде можно записать так:
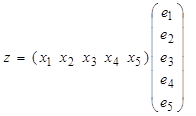 ,
, 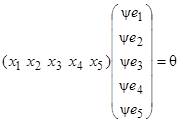 ,
,
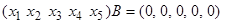 ;
;
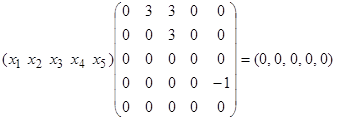 ;
; 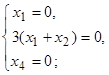
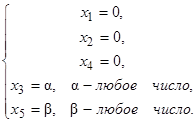
Таким образом, если  , то
, то  , т.е.
, т.е.
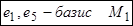 .
.
Пусть 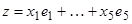 ,
, 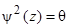 . Повторив рассуждения, получим
. Повторив рассуждения, получим 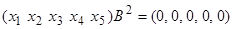 , где
, где
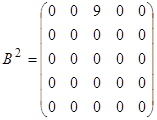 .
.
Для нахождения координат 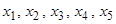 вектора z при условии
вектора z при условии 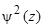 необходимо решить систему:
необходимо решить систему:
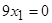 ,
,
т.е. 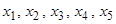 – любые числа. Это означает, что
– любые числа. Это означает, что
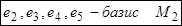 .
.
Так как 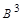 – нулевая матрица, то условию
– нулевая матрица, то условию 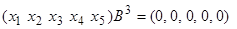 удовлетворяют все векторы линейного пространства, т.е.
удовлетворяют все векторы линейного пространства, т.е.
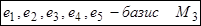 .
.
Перейдем к построению относительных базисов.
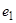 – базис М 3относительно М 2,
– базис М 3относительно М 2,
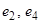 – базис М 2относительно М 1.
– базис М 2относительно М 1.
В базисе М 2можно заменить е2 на 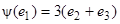 . Тогда
. Тогда 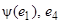 – базис М 2относительно М 1. Векторы
– базис М 2относительно М 1. Векторы 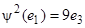 ,
, 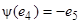 линейно независимы в М 1и их можно взять в качестве базиса М 1. Объединение относительных базисов – базис корневого пространства.
линейно независимы в М 1и их можно взять в качестве базиса М 1. Объединение относительных базисов – базис корневого пространства.
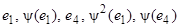 – базис V.
– базис V.
Расположим эти векторы несколько в ином порядке
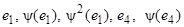 .
.
Линейный оператор 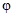 действует в этом базисе так:
действует в этом базисе так:
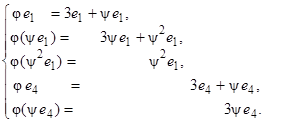
Матрица линейного оператора 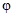 в этом базисе имеет канонический вид – состоит из двух клеток Жордана
в этом базисе имеет канонический вид – состоит из двух клеток Жордана
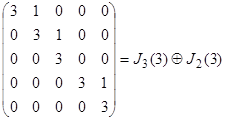 .
.
Следовательно, 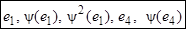 – канонический базис.
– канонический базис.