Канонический базис

Клеткой Жордана называется матрица вида

, где k ³ 1, J₁(r) = r.

Матрицей Жордана называется клеточно-диагональная матрица вида:

.

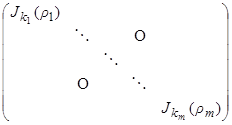Для такой матрицы введем обозначение:

.

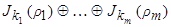Если все клетки первого порядка, то матрица Жордана диагональная.

Базис линейного пространства называется каноническим относительно линейного оператора j, если матрица линейного оператора j в этом базисе – матрица Жордана.

Теорема. Если характеристический многочлен c(l)линейного оператора j, действующего в конечномерном линейном пространстве над полем К, целиком раскладывается на линейные множители, то в этом линейном пространстве существует канонический базис.

Доказательство следует из построений, которые приведены в следующих параграфах.

Заметим, что из этой теоремы и из основной теоремы алгебры комплексных чисел следует, что в линейных пространствах над полем комплексных чисел канонический базис существует для любого линейного оператора. ■