
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Корневые векторы
|
|
Пусть r – собственное значение линейного оператора j, действующего в линейном пространстве V/K, e –тождественный линейный оператор, т.е. e(а) = а " а Î V. Вектор с называется корневым вектором линейного оператора j, принадлежащим собственному значению r, если существует натуральное число s, для которого
(j - re) sс = q.(1)
Из этого условия следует, что (j - re) tс = qдля любого натурального числа t > s. Наименьшее натуральное число s, для которого выполнено условие (1) называется высотой корневого вектора с. Высотой нулевого вектора считаем нуль. Ненулевой собственный вектор – это корневой вектор высоты 1, т.е. корневой вектор – это обобщение понятия собственного вектора.
Теорема. Ненулевые корневые векторы, принадлежащие различным собственным значениям, различны.
Доказательство. Пусть r1и r2 – два разных собственных значения линейного оператора j, с – принадлежащий им общий ненулевой корневой вектор:
(j - r1e) nc = q, (j - r2e) mc = q.
Так как r1 ¹ r2, то многочлены (х - r1) n и (х - r2) m взаимно простые и по теореме о линейном представлении НОД существуют многочлены u (x) и v (x) из K [ x ], для которых
u (x) (х - r1) n + v (x) (х - r2) m = 1.
Отсюда
u (j) (j - r1e) n + v (j) (j - r2e) m = e Þ
Þ с = e(с) = u (j) (j - r1e) nс + v (j) (j - r2e) mс = u (j)q + v (j)q = q.
Получили противоречие с тем, что с – ненулевой вектор. ■
Теорема. Ненулевые корневые векторы, принадлежащие различным собственным значениям, линейно независимы.
Доказательство. Пусть r1,..., r m – различные собственные значения линейного оператора j; с 1 ,..., сm – ненулевые корневые векторы, принадлежащие этим собственным значениям; h 1,..., hm - их высоты соответственно.
Методом полной математической индукции по числу векторов m докажем линейную независимость векторов с 1 ,..., сm. При m =1утверждение верно, так как один ненулевой вектор образует линейно независимую систему. Предположим, что утверждение верно при m = k. Пусть m= k +1и l1 с 1 +... + l kck + l k +1 ck +1= q.Применим к обеим частям равенства линейный оператор (j - r k +1e) 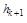 .Получим
.Получим
l1(j - r k +1e) 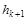 с 1 +... + l k (j - r k +1e)
с 1 +... + l k (j - r k +1e) 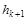 ck = q.
ck = q.
По предыдущей теореме векторы
(j - r k +1e) 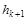 с 1,..., (j - r k +1e)
с 1,..., (j - r k +1e) 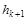 сk
сk
ненулевые, причем они являются корневыми векторами, принадлежащими различным собственным значениямr1,..., r k .Проверим, к примеру, что первый из них принадлежит первому собственному значению.
(j - r1e) 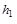 ((j - r k +1e)
((j - r k +1e) 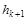 с 1) = (j - r k +1e)
с 1) = (j - r k +1e) 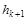 ((j - r1e)
((j - r1e) 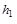 с 1) =
с 1) =
= (j - r k +1e) 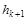 q = q.
q = q.
Заметим, что композиция отображений некоммутативна, но многочлены от одного и того же отображения перестановочны. Чем мы и воспользовались при проведении данных выкладок. По гипотезе индукции l1 = 0,..., l k = 0 Þ l k +1 ck +1 = q Þ l k +1 = q.Векторы с 1,..., сk +1 линейно независимы. ■