Множества.

Множество – совокупность некоторых объектов определенной природы. Объекты, образующие множество, называются его элементами.

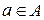- элемент 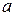принадлежит множеству .

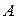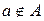- элемент 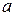не принадлежит множеству .

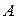Задать множество можно перечислением его элементов 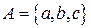; с помощью некоторой процедуры 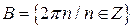; при помощи описания свойств элементов, входящих в множество, .

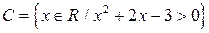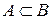- множество 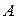является подмножеством 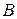, т. е. каждый элемент множества 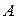является элементом множества .

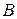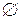- пустое множество. Множество, состоящее из 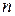элементов, содержит с учетом пустого подмножества 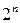подмножеств.

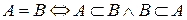- равные множества.

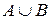- множество, элементы которого являются элементами множества 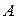или множества 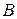или элементами обоих множеств (объединение множеств).

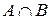- множество, элементы которого являются элементами множества 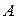и одновременно элементами множества 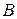(пересечение множеств).

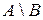- множество, элементы которого являются элементами множества 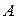, не принадлежащие множеству 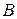(разность множеств).

Множества 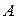и 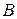называются эквивалентными, если между элементами множеств можно установить взаимно однозначное соответствие. Конечные множества эквивалентны тогда и только тогда, когда они содержат одинаковое количество элементов.

В случае бесконечного множества эквивалентными могут быть все множество и его подмножество. Например, с помощью процедуры 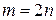мы можем установить взаимно однозначное соответствие между множеством натуральных чисел и множеством четных натуральных чисел, т. е. установить их эквивалентность.

Счетное множество – множество, эквивалентное множеству натуральных чисел. Можно показать, что счетным множеством является множество рациональных чисел. Множество иррациональных чисел не является счетным.