Непрерывность функции.

Определение. Функция непрерывна в точке 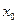, если она определена в некоторой окрестности этой точки, в том числе и в самой тоске 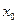, и если 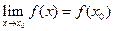, т.е. .

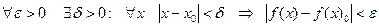Из определения следует, что для непрерывной функции справедливо равенство:

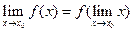, то есть предел можно вносить в аргумент непрерывной функции.

Определение*. Функция непрерывна в точке 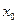, если она определена в некоторой окрестности этой точки, в том числе и в самой тоске 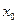, и если ее приращение в этой точке, соответствующее приращению аргумента 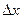, стремится к нулю при , т.е. .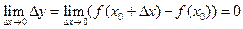

Пример. Функция 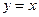непрерывна для любого .

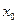Действительно .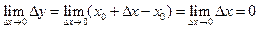

Пример. Функция 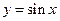непрерывна для любого .

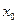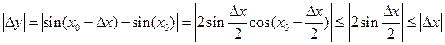. Здесь мы использовали неравенство 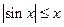. Таким образом, имеем 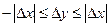, т.е. функция 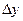зажата между двумя функциями, стремящимися к нулю. Значит, и 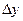стремится к нулю.

Теорема. Если и 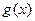непрерывны в точке 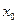, то непрерывны их сумма, разность, произведение и частное.

Доказательство. Доказательство вытекает из определения непрерывности 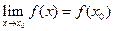и теоремы о пределах суммы, разности, произведения и частного.

Теорема. (О непрерывности сложной функции). Пусть задана функция , непрерывная в точке 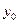, и функция 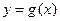, непрерывная в точке 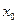, и пусть . Тогда сложная функция 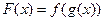непрерывна в точке .

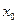Доказательство. .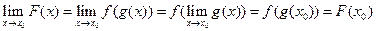

Пример. Многочлен 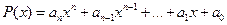- непрерывная функция, т.к. является результатом конечного числа арифметических операций над непрерывной функцией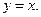

Пример. 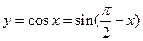- сложная функция.

Пример. 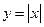- непрерывная функция.

Действительно: ; .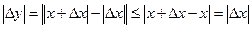

Пример. Если непрерывна, то непрерывна и сложная функция 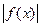.