Числовая последовательность.

Определение. Числовая последовательность –бесконечное множество пронумерованных чисел. Каждый элемент последовательности характеризуется номером и своим значением.

Примеры последовательностей: ; ; ; ; .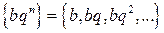

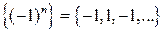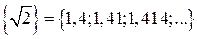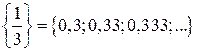Определение*. Числовая последовательность –функция, заданная на множестве натуральных чисел.

Определение. Последовательность неубывающая, если

Определение. Последовательность ограничена сверху, если

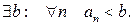
Определение. Последовательность не ограничена сверху, если (отрицание к предыдущему определению)

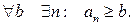
Определение. Число 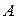называется пределом последовательности 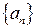, если

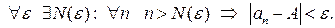
Это записывается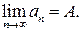

Рассмотрим неравенство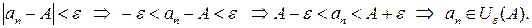

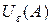- окрестность точки 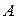размера 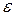(интервал с центром в точке 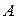и длиной ).

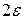Определение*. 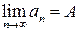, если

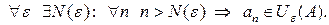
Теорема. Если 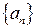имеет предел, то он единственный.

Доказательство. Пусть 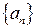имеет два предела 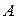и 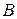. Возьмем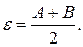

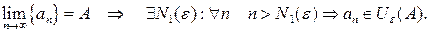
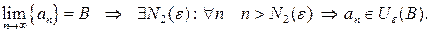
Мы получили, что начиная с номера 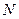, который больше 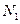и 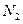, все члены последовательности лежат в окрестности тоски 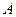и в окрестности точки 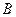. Противоречие, т.к. окрестности точек 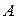и 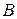не пересекаются. Теорема доказана.

Теорема. Если 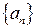имеет конечный предел, то она ограничена.

Доказательство. Пусть 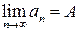. Возьмем 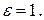найдем 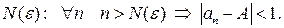Из последнего неравенства следует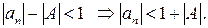

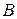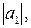
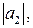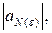
Пусть наибольшее среди чисел …, 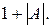Тогда 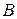превосходит модуль всех членов нашей последовательности, т.е. последовательность ограничена. Теорема доказана.

Определение. Последовательность, имеющая конечный предел, называется сходящейся последовательностью или фундаментальной последовательностью.

Теорема. Если 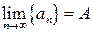, , 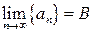то

;

;

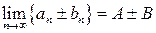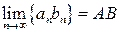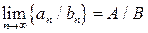
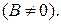
Доказательство. Докажем выражение для произведения. Так как 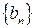имеет конечный предел, то она ограничена некоторым числом 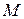. Пусть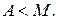

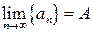
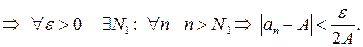
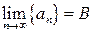
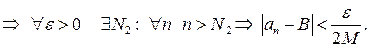
Для того чтобы доказать 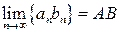, надо показать, что для любого 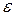найдется номер 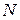, такой, что для всех 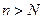выполняется неравенство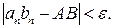

.

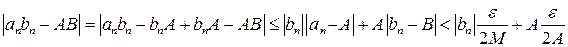Начиная с любого номера 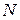, который больше 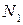и 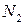сумма в правой части неравенства меньше 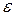. Теорема доказана.

Пример. Показать, что 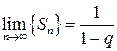, где 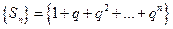- геометрическая прогрессия при .

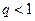Заметим, что 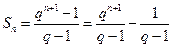. Так как 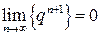, используя теорему о пределах суммы, произведения и частного, получаем требуемый результат.

Пример. Показать, что .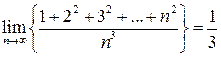

Если 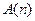верное утверждение для числа 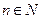, тогда принцип математической индукции заключается в следующем: .

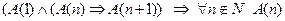По индукции доказываем, что 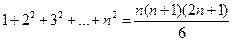. Делим числитель и знаменатель последовательности на 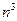и получаем нужный результат.

Определение. Число 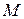называется точной верхней гранью последовательности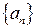 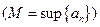, если .

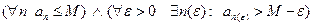Теорема. Всякая ограниченная сверху последовательность 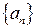имеет предел, причем .

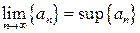Доказательство. Так как последовательность ограничена сверху она имеет точную верхнюю грань 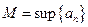, значит 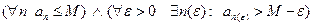. В силу неубывания последовательности 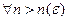имеем: 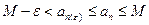; ; 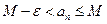; 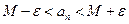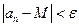. Таким образом, 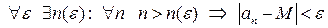, т.е. 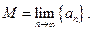Теорема доказана.