
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Функции, непрерывные на отрезке.
|
|
Определение. Функция  непрерывна на отрезке
непрерывна на отрезке  , если она непрерывна во всех точках интервала
, если она непрерывна во всех точках интервала 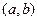 , а
, а  и
и  .
.
Теорема. Если функция  непрерывна на отрезке
непрерывна на отрезке  , то она ограничена, т.е.
, то она ограничена, т.е.  .
.
Доказательство. Допустим, что функция  не ограничена на отрезке
не ограничена на отрезке  . Тогда
. Тогда  . Берем последовательно
. Берем последовательно 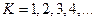 , получим:
, получим: 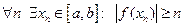 . Заметим, что
. Заметим, что  . Последовательность
. Последовательность  ограничена, т.к.
ограничена, т.к.  . По теореме Больцано-Вейерштрасса из
. По теореме Больцано-Вейерштрасса из  можно выбрать сходящуюся подпоследовательность
можно выбрать сходящуюся подпоследовательность  , т.е.
, т.е. 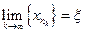 , где
, где  . В силу непрерывности
. В силу непрерывности  имеем:
имеем:  , где
, где  конечное число, согласно нашему предположению. Но мы уже получили, что
конечное число, согласно нашему предположению. Но мы уже получили, что  , а значит,
, а значит,  . Противоречие. Теорема доказана.
. Противоречие. Теорема доказана.
Теорема. (Вейерштрасса). Если функция  непрерывна на отрезке
непрерывна на отрезке  , то существует ее минимум и максимум на
, то существует ее минимум и максимум на  , т.е. существуют точки
, т.е. существуют точки 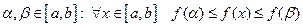 .
.
Доказательство. Докажем для максимума. По предыдущей теореме непрерывная на отрезке  функция ограничена сверху некоторым числом
функция ограничена сверху некоторым числом  , но тогда существует точная верхняя грань
, но тогда существует точная верхняя грань  , т.е.
, т.е. 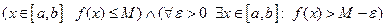 . Полагая последовательно
. Полагая последовательно 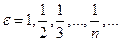 , получаем последовательность
, получаем последовательность  , такую, что
, такую, что 

 . Так как последовательность
. Так как последовательность  ограничена, то существует подпоследовательность
ограничена, то существует подпоследовательность  сходящаяся к
сходящаяся к 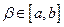 . В силу непрерывности нашей функции
. В силу непрерывности нашей функции 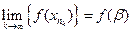 . Если предел существует, то он единственный, т.е.
. Если предел существует, то он единственный, т.е. 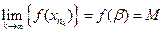 .
.
Таким образом, точная верхняя грань достигается функцией в точке 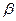 , т.е. в точке
, т.е. в точке 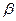 функция принимает свое максимальное значение. Теорема доказана.
функция принимает свое максимальное значение. Теорема доказана.
Теорема. (О нулях непрерывной на отрезке функции). Если функция  непрерывна на отрезке
непрерывна на отрезке  и принимает на его концах значения разных знаков, то на интервале
и принимает на его концах значения разных знаков, то на интервале  имеется, по крайней мере, одна точка
имеется, по крайней мере, одна точка  , такая, что
, такая, что 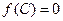 .
.
Доказательство. Обозначим отрезок  через
через 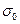 . Разделим его пополам. Если в середине
. Разделим его пополам. Если в середине 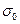 функция равна нулю, то теорема доказана. Если этого нет, то одна из половинок такая, что на концах функция имеет значения разных знаков. Обозначим именно эту половинку через
функция равна нулю, то теорема доказана. Если этого нет, то одна из половинок такая, что на концах функция имеет значения разных знаков. Обозначим именно эту половинку через 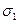 . Продолжим эту процедуру. Мы либо наткнемся на точку
. Продолжим эту процедуру. Мы либо наткнемся на точку  , такую, что
, такую, что 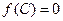 , либо получим систему вложенных стремящихся к нулю отрезков. Система таких отрезков по аксиоме непрерывности имеет общую точку
, либо получим систему вложенных стремящихся к нулю отрезков. Система таких отрезков по аксиоме непрерывности имеет общую точку  . Покажем, что
. Покажем, что 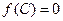 .
.
Пусть, например,  . Но тогда по теореме о сохранении знака непрерывной функции
. Но тогда по теореме о сохранении знака непрерывной функции 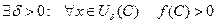 . С другой стороны, для
. С другой стороны, для 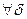 мы можем указать вложенный отрезок
мы можем указать вложенный отрезок  , где
, где  принимает разные знаки на концах отрезка. Противоречие.
принимает разные знаки на концах отрезка. Противоречие.
Предположение  тоже приводит к противоречию. Тогда по аксиоме порядка
тоже приводит к противоречию. Тогда по аксиоме порядка 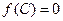 . Теорема доказана.
. Теорема доказана.
Вопросы к коллоквиуму по математическому анализу (1 семестр)
1.Множество действительных чисел.
2.Теорема о точной грани ограниченного множества.
3.Понятие числовой последовательности. Ее предел.
4.Единственность предела. Ограниченность сходящейся последовательности.
5.Арифметические операции над сходящимися последовательностями.
6.Точная верхняя грань последовательности. Теорема о пределе ограниченной сверху неубывающей последовательности.
7.Число е.
8.Теорема Больцано-Вейерштрасса.
9.Критерий Коши существования конечного предела последовательности.
10.Понятие функции действительного переменного. Предел функции.
11.Эквивалентность определений предела по Коши и по Гейне.
12. Критерий Коши существования предела функции.
13.Теорема об ограниченности функции, имеющей конечный предел.
14.Теорема о сохранении знака функции, имеющей конечный предел.
15.Теорема о зажатой функции.
16.Непрерывность функции. Непрерывность сложной функции.
17.Классификация точек разрыва. Примеры.
18.Замечательные пределы.
19.Сравнение бесконечно малых.
20.Ограниченность функции, непрерывной на отрезке.
21.Теорема Вейерштрасса.
22.Теорема о нулях непрерывной на отрезке функции.
