Методы определения порядка реакции. Существует несколько способов нахождения частного порядка и порядка реакции.

Существует несколько способов нахождения частного порядка и порядка реакции.

Метод подбора кинетического уравнения. Экспериментальные данные зависимости концентрации реагируемого вещества от времени подставляют в различные кинетические уравнения первого (5.5), второго (5.6) и n -го (5.9) порядков.

Если рассчитанные значения константы скорости, например, по уравнению (5.5) сохраняются постоянными (в пределах погрешностей опыта), то порядок исследуемой реакции будет первым.

Графический метод. Порядок реакции можно определять графическим методом. Ниже приведены дифференциальные уравнения скоростей реакций различных порядков и их решения.

Порядок	Уравнение скорости реакции	Решение уравнения
		ln c = ln c 0- kt
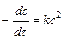
		1/ c = 1/ c 0 + kt
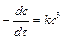
		1/ c2= 1/(c 0)2 + 2 kt

Отложив на оси ординат ln с, 1/ с и 1/ с², ана оси абсцисс время t, для изучаемой реакции получают три линии. Та из них, которая является прямой, соответствует порядку данной реакции.

Метод определения порядка реакции по времени полупревращения. Для реакции n -го порядка (n ¹ 1) время полупревращения выражается соотношением (5.10).

Произведение времени полупревращения на кинетически активную начальную концентрацию исходного вещества с ⁰, возведенную в степень (n - 1), является постоянной

.

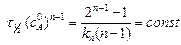Следовательно, для двух начальных концентраций исходного вещества, можно записать

(5.14)

После логарифмирования выражения (5.14) определяют порядок реакции

.

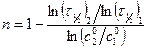Для графического решения указанного способа используют выражение (5.10) в логарифмической форме

.

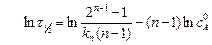Строя зависимость от 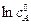, находят порядок реакции по угловому коэффициенту прямой и константу скорости по отрезку, отсекаемому построенной прямой на оси ординат.

Время полупревращения реакции первого порядка не зависит от начальной концентрации исходного вещества. Следовательно, на основании опытных данных 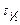не зависит от начальной концентрации реагента, реакция имеет первый порядок.

Метод Оствальда – Нойеса основан на определении времени, в течение которого концентрация вещества уменьшается в определенное число раз. При допущении, что скорость реакции при концентрациях реагентов, пропорциональных их стехиометрическим коэффициентам в уравнении химической реакции (или при избытке всех реагентов, кроме одного), соответствует уравнению (5.10) и с учетом с ⁰ – с = aс ⁰после преобразования, имеют

.

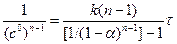Для двух кинетических опытов, протекающих до одной и той же степени превращения (a ₁ = a ₂),

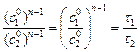, (5.15)

где 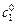и 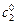– начальные концентрации реагирующих веществ в опыте 1 и 2; t ₁ и t ₂ – время протекания реакции в двух опытах до одной и той же степени превращения a.

После логарифмирования уравнения (5.15) получают

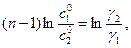
. (5.16)

Уравнение (5.16) справедливо, если реакцию проводят до любой степени превращения.

В таблице (5.1) представлены значения времени превращения исходного вещества на определенную долю для различных порядков реакции.

Т а б л и ц а 5.1

Порядок	Время превращения t 1/x
t 1/2	t 1/3	t 1/4
	c 0/2 k	c 0/3 k	c 0/4 k
	ln2/ k	ln(3/2)/ k	ln(4/3)/ k
	1/ kc 0	1/2 kc 0	1/3 kc 0
	3/2 k (c 0)2	5/8 k (c 0)2	7/18 k (c 0)2
n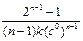

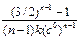
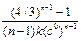
Метод изолирования Оствальда. Этот метод определения порядка реакции по каждому из веществ называют также методом понижения порядка реакции.

Если реакция А+В ® С протекает при различных начальных концентрациях исходных веществ, кинетический закон действующих масс примет вид

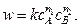
Суть метода состоит в том, что проводят изучение зависимости скорости реакции от начальной концентрации одного из исходных веществ (например A), остальные вещества берутся в большом избытке. В этом случае кинетический закон упрощается

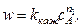
если с_В > > с_А; 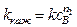– величина кажущийся константы скорости зависит от концентрации вещества В. Порядок реакции n ₁ по веществу А находят одним из рассмотренных выше способов. Определяя затем при постоянной температуре численные значения k_каж для различных значений 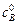( 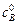> > 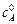), можно алгебраическим или графическим путем рассчитать порядок реакции n ₂ по веществу В и константу скорости по уравнению

.

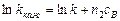Зная порядки по отдельным веществам, находят и общий порядок реакции (n = n₁ + n₂).

Метод Вант-Гоффа. В этом методе используется дифференциальная форма кинетического уравнения

.

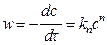Логарифмируя это уравнение при условии малой степени превращения (с» с ⁰), получают уравнение прямой линии

,

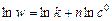тангенс угла наклона которой равен порядку реакции n.

Метод определения порядка реакции по начальным концентрациям. Порядок реакции n может быть также рассчитан на основании данных двух кинетических опытов с начальными концентрациями реагирующих веществ 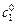и 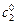по уравнению

.

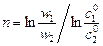При расчетах n величину –(dc/dτ) удобнее заменять на (–Δ с /Δ τ).