
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение угла атаки и вычисление левых частей уравнений
|
|
Траекторию полета ЛА условно можно разделить на три, резко отличающихся друг от друга участка: стартовый, ввод в режим наведения и непосредственно наведение ЛА на цель. В ряде случаев некоторые из них могут продолжаться очень короткое время, а иногда и совсем отсутствовать.
Система уравнений движения ц.м. ЛА на всех этих участках формально выглядит одинаково:
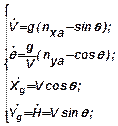
где 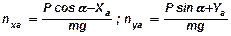 .
.
Уравнение для определения массы ЛА исключено, так как исследуемые ЛА имеют однорежимные ракетные двигатели. Масса ЛА может быть легко определена в любой момент времени: В данном случае на активном участке траектории (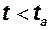 ) масса ЛА определяется по формуле
) масса ЛА определяется по формуле 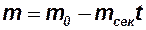 .
.
На каждом из этих участков будут различными условия замыкания, а при движении ЛА по направляющим ещё необходимо учесть и дополнительные силы. При решении рассматриваемых задач встречается три вида замыканий: задается угол атаки 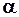 , величина нормальной скоростной нагрузки
, величина нормальной скоростной нагрузки 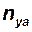 или величина угловой скорости вращения вектора скорости
или величина угловой скорости вращения вектора скорости 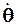 . Причем третий вариант замыкания может рассматриваться как аналогичный второму, так как:
. Причем третий вариант замыкания может рассматриваться как аналогичный второму, так как:
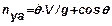 ,
,
а по известному значению 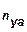 можно определить необходимый угол атаки. Для данной системы уравнений единственным управляющим фактором является угол атаки. Так как все аэродинамические коэффициенты зависят не линейно от угла атаки, то его значение можно определить графически или путём итераций.
можно определить необходимый угол атаки. Для данной системы уравнений единственным управляющим фактором является угол атаки. Так как все аэродинамические коэффициенты зависят не линейно от угла атаки, то его значение можно определить графически или путём итераций.
В процессе замыкания этой системы должен быть определён угол атаки и в этом случае правые части этой системы легко определяются и, следовательно, система может быть проинтегрирована (числено).
При решении поставленных задач интегрируется система упрощённых уравнений, описывающих движение центра масс ЛА в вертикальной плоскости. Единственным управляющим фактором этой системы является угол атаки. Причём идеальная система уравнений позволяет даже мгновенное изменение этого параметра, как и некоторых других (например, тяги силовой установки). Даже при таких упрощениях она представляет систему нелинейных дифференциальных уравнений, которую можно численно проинтегрировать при соответствующих замыкающих условиях. Существует много различных методов численного интегрирования. Но при использовании любого из этих методов основную трудоёмкость представляет вычисление правых частей этих уравнений, т.е. численное определение значений производных при заданных условиях.
В процессе численного интегрирования системы уравнений движения центра масс ЛА необходимо на каждом шаге вычислять правые части этих уравнений, т.е. определять численные значения производных интересующих нас величин. Эти вычисления удобно выполнять в таблицах. Например, табл 4.1.
Таблица 4.1. – Таблица численного интегрирования
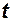
| 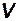
| 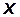
| 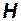
| 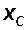
| 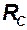
| 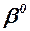
| 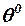
| 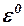
|
| с | м/с | м | м | м | м | градусы |
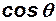
| 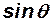
| 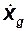
| 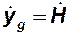
| 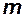
| 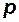
| 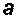
| 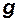
| 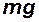
|
| — | — | м/с | м/с | кг | Па | м/с | м/с2 | н |
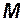
| 
| 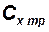
| 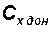
| 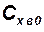
| 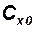
| 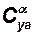
| 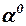
| 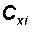
|
| — | н | — | — | — | — | — | градус | — |
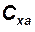
| 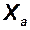
| 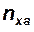
| 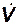
| 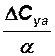
| 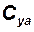
| 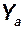
| 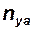
| 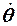
|
| — | н | — | м/c2 | — | — | н | — | c-1 |
В данный момент времени известны (или могут быть найдены) практически все параметры ЛА и цели, а также среды, в которых происходит их движение. Для данной системы уравнений угол атаки является единственным управляющим фактором, и дальнейшее движение ЛА фактически зависит только от него. Только определив закон изменения угла атаки, можно рассчитать движение ЛА на этом шаге.
Физический смысл и формулы для вычислений основных параметров в этой таблице. В [1] располагается время полета, а в [2], [3] и [4] — скорость и координаты расположения ЛА. Здесь и далее в квадратных скобках указан номер столбца (колонки). В [5] столбце указана горизонтальная составляющая координата цели. Рассматривается только равномерный горизонтальный полет цели, и поэтому скорость и высота полета цели не изменяются 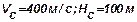 . Поэтому они не включены в таблицу. По этой же причине в таблицу также не включена и тяга ЛА. Однако следует не забывать, что значение тяги в момент отсечки мгновенно уменьшается и затем остаётся равным нулю. При неработающем двигателе появляется так называемое донное сопротивление.
. Поэтому они не включены в таблицу. По этой же причине в таблицу также не включена и тяга ЛА. Однако следует не забывать, что значение тяги в момент отсечки мгновенно уменьшается и затем остаётся равным нулю. При неработающем двигателе появляется так называемое донное сопротивление.
Горизонтальная координата цели [5], а также расстояние между целью и перехватчиком вычисляются по следующим формулам:
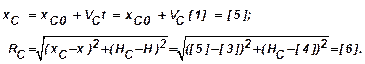
Значение угла визирования:
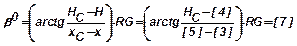
Здесь и далее 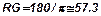 — коэффициент для перевода угловых значений из радиан в градусы. Значения угла упреждения
— коэффициент для перевода угловых значений из радиан в градусы. Значения угла упреждения 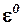 вычисляются через
вычисляются через 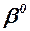 и
и 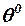 :
:
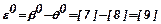 .
.
Первые девять величин являются как бы начальными условиями для следующего шага интегрирования: перед началом расчёта они задаются (их значения можно взять из распечатки), а затем — получаются при интегрировании.
В следующих четырёх колонках записываются значения косинуса и синуса угла наклона траектории к горизонту и вычисляются правые части третьего и четвёртого уравнений:
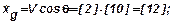
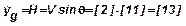 .
.
Следующие три параметра [15], [16] и [17] характеризуют среду (давление, скорость звука и ускорение земного притяжения) и определяются по графикам, построенным по данным таблицы 1.1 для нужного диапазона высот.
Далее определяются (вычисляются) вес ЛА, число 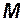 и произведение скоростного напора на характерную площадь:
и произведение скоростного напора на характерную площадь:
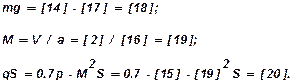
Для соответствующих параметров полёта (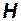 и
и 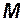 ) с графиков снимаются значения коэффициентов трения {
) с графиков снимаются значения коэффициентов трения { 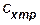 } и донного сопротивления {
} и донного сопротивления { 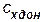 }.
}.
Коэффициент 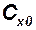 лобового сопротивления при
лобового сопротивления при 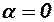 равен сумме этих составляющих:
равен сумме этих составляющих:
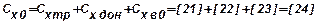 .
.
Далее для данного числа 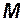 определяется по графикам величина производной коэффициента подъёмной силы по углу атаки
определяется по графикам величина производной коэффициента подъёмной силы по углу атаки 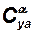 .
.
Угол атаки можно определить, используя следующую итерационную формулу:
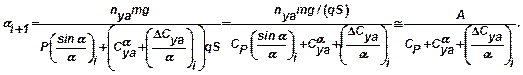
Для метода совмещения итерации удобно выполнять в следующей последовательности:
1. Задаём начальное значение угла атаки  , если расчёт только начинается, то можно принять, что
, если расчёт только начинается, то можно принять, что 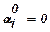 , если расчёт продолжается, то в качестве начального приближения значения угла атаки удобно принимать его значение на предыдущем шаге;
, если расчёт продолжается, то в качестве начального приближения значения угла атаки удобно принимать его значение на предыдущем шаге;
2. Далее выполняем операции с колонками [27] – [31] табл. 4.1, по углу атаки определяем значение коэффициента индуктивного сопротивления, коэффициента и силы лобового сопротивления, тангенциальной перегрузки и параметра 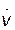 , вычисляем значение параметра
, вычисляем значение параметра 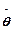 , а затем и величину нормальной скоростной перегрузки
, а затем и величину нормальной скоростной перегрузки 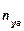 ;
;
3. По вычисленному значению 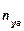 определяем числитель итерационной формулы:
определяем числитель итерационной формулы:
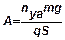 ;
;
4. По углу атаки определяем коэффициент  ;
;
5. Вычисляем знаменатель итерационной формулы;
6. Определяем итерационное значение угла атаки;
7. Сравнивая полученное значение угла атаки с предыдущим, определяем погрешность. Если заданная точность не достигнута, то необходимо повторить весь процесс вычисления, начиная с пункта 2, приняв вычисленное значение угла атаки за начальное. Процесс продолжается до достижения заданной точности.
Для проведения итераций в этом случае удобно воспользоваться таблицей 4.2.
 Таблица4.2 – Определение угла атаки
Таблица4.2 – Определение угла атаки
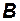
| 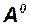
| 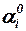
| 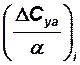
| 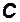
| 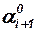
| ......... |
| — | градус | градус | — | — | градус |
Здесь 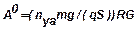 ;
; 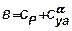 ;
; 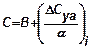 и
и 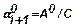 .
.
Фактически здесь итерационный процесс протекает между 103 и 105 столбцами или их аналогами, так как при этом другие величины остаются без изменения.
По приведенному выше алгоритму находим угол атаки 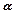 . По
. По 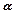 и М находим
и М находим 
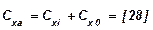 ;
;
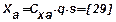 ;
;
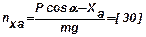 ;
;
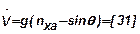 ;
;
Значение 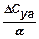 определяем из графиков.
определяем из графиков.
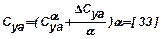 ;
;
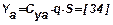 ;
;
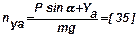 ;
;
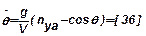 .
.
Дальнейшие операции зависят от используемого метода интегрирования.