Определение схемных функций методом эквивалентных схем на основе координатных уравнений для координат (КК-уравнений) в узловом координатном базисе.

При математическом описании электронной схемы в узловом координатном базисе все компоненты схемы замещения должны быть представлены как y-компоненты: задающие источники – независимыми источниками тока, зависимые источники – источниками тока, управляемыми напряжениями, пассивные двухполюсники – соответствующими проводимостями.

Для удобства формирования схемы замещения избирательного усилителя предварительно преобразуем компоненты эквивалентных схем биполярных транзисторов к y-компонентам.

В эквивалентной схеме для системы h-параметров транзистора, включенного с общим коллектором (рис. 6.2, а), зависимый источник напряжения 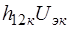, управляемый напряжением 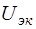, с последовательно включенным сопротивлением 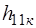преобразуется в зависимый источник тока 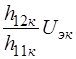, управляемый напряжением 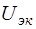, с параллельно включенной проводимостью .

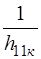Управляющий ток 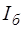зависимого источника тока 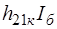, управляемого током, можно представить выражением 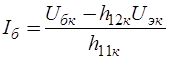, тогда управляемый ток источника зависит от двух напряжений 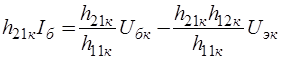, а сам источник 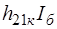может быть представлен отдельными источниками тока 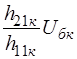и 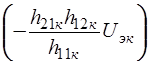, управляемыми напряжениям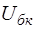и и 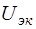. Полученная в результате эквивалентная схема биполярного транзистора представлена на рис. 6.16.

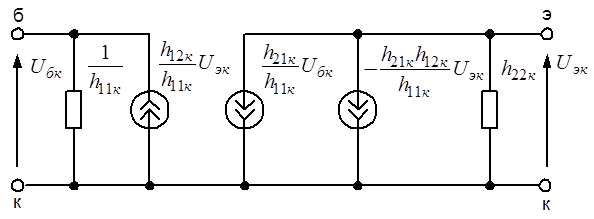
Рис. 6.16. Модифицированная эквивалентная схема биполярного транзистора

Поскольку зависимый источник тока 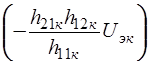управляется напряжением 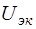, действующим на ветви самого источника тока, этот источник может быть представлен эквивалентным двухполюсным компонентом с проводимостью 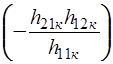. Представляя параллельно включенные ветви с проводимостям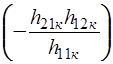и и 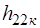одной эквивалентной ветвью, а также изменяя направление зависимого источника тока 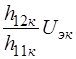, получим эквивалентную схему рис. 6.17.

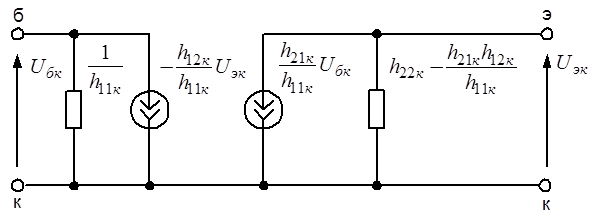
Рис. 6.17. Эквивалентная схема биполярного транзистора с общим коллектором, приведенная к системе y-параметров

Эквивалентная схема рис. 6.17, соответствует системе y-параметров транзистора, включенного с общим коллектором, и может быть представлена в виде рис. 6.18, где , , , .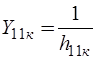

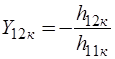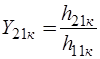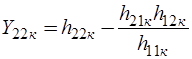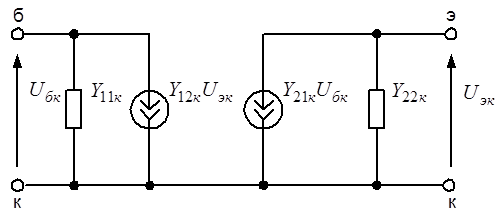
Рис. 6.18. Эквивалентная схема биполярного транзистора с общим коллектором в системе y-параметров

В низкочастотной Т-образной физической эквивалентной схеме (рис. 6.2, б) управляющий ток 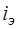представим выражением 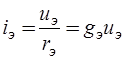, а зависимый источник тока 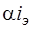, управляемый током, преобразуем в зависимый источник тока 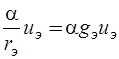, управляемый напряжением 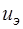(рис. 6.19).

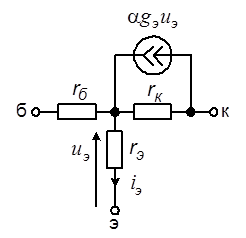
Рис. 6.19. Физическая Т-образная эквивалентная схема биполярного транзистора с источником тока, управляемым напряжением

Используя эквивалентные схемы биполярных транзисторов, представленные на рис. 6.18, 6.19, получим схему замещения избирательного усилителя по переменному току для полного диапазона частот, приведенную на рис. 6.20.

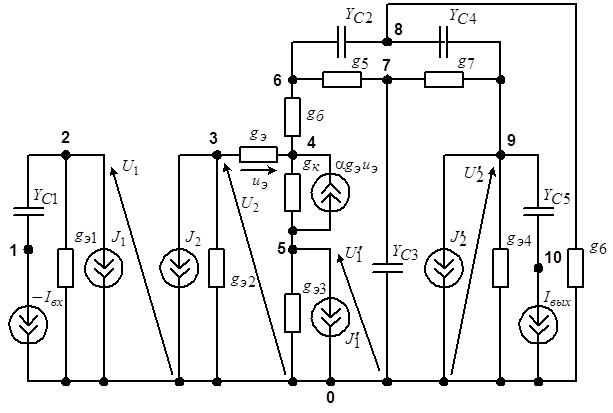
Рис. 6.20. Схема замещения избирательного усилителя, содержащая двухполюсные компоненты

В схеме замещения рис. 6.20: , , , , , , , , , , , , , , , , , , .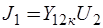

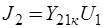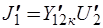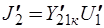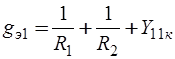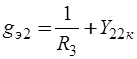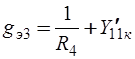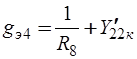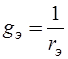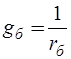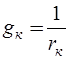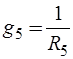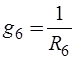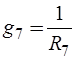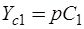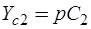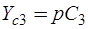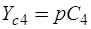Полюсный граф избирательного усилителя, соответствующий схеме замещения рис. 6.20, представлен на рис. 6.21, причем все ребра графа отнесены к y-ребрам.

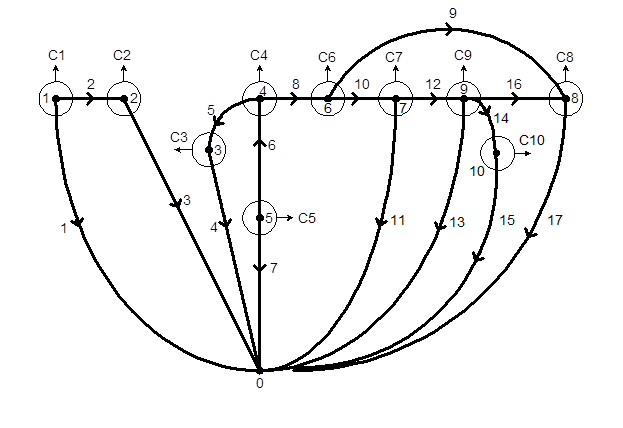
Рис. 6.21. Полюсный граф избирательного усилителя с канонической системой независимых сечений

Система координат представляет собой совокупность 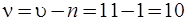независимых сечений. Выберем каноническую систему сечений, обозначенную на рис. 6.21.

Матрица независимых сечений имеет размерность :

.

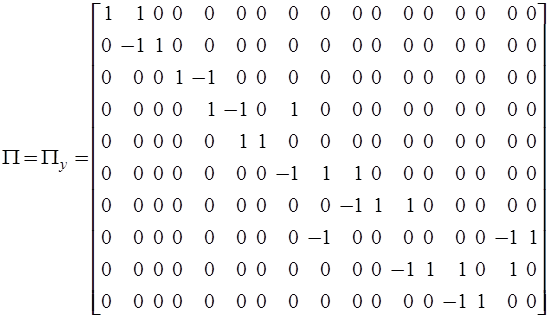Матрично-векторные параметры обобщенного топологического уравнения имеют вид 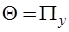, , 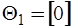, 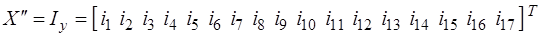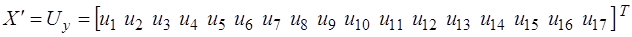а уравнение (6.1) преобразуется к виду

.

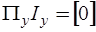Матрично-векторные параметры обобщенного компонентного уравнения определяются соотношениями 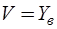, , 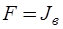в результате чего обобщенное компонентное уравнение (6.2) приводится к виду

.

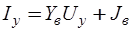Матрица 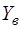проводимостей y-ребер и управляющих проводимостей источников тока, управляемых напряжениями, является квадратной матрицей 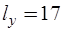порядка:

.

Вектор 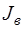задающих токов ветвей содержит 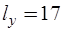компонентов:

.

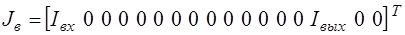В узловом координатном базисе координатные уравнения для координат принимают частный вид узловых уравнений:

,

где 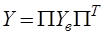- матрица проводимостей электронной схемы; 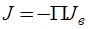- вектор задающих токов независимых сечений.

При использовании канонической системы сечений связь схемных функций с матрицей проводимостей электронной схемы определяется выражениями:

,

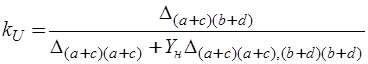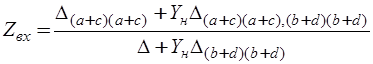, (6.49)

.

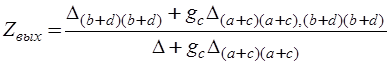Для обозначенной на рис. 6.21 канонической системы независимых сечений 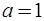, , 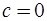, , 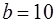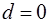и выражения (6.49) принимают вид:

,

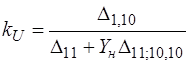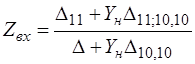, (6.50)

.
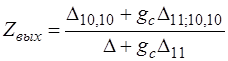