Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод найменших квадратів
|
|
Нехай на вхід деякого пристрою подається сигнал x, а на виході вимірюється сигнал у. Відомо, що величини x і у зв'язані функціональною залежністю, але якою саме - невідомо. Потрібно приблизно визначити цю функціональну залежність y = φ (x) за дослідними даними. Нехай в результаті n вимірювань отриманий ряд експериментальних точок (xi, yi). Відомо, що через n точок можна завжди провести криву, що аналітично виражається многочленом (n - 1) -го ступеня. Цей многочлен називають інтерполяційним. І взагалі, заміну функції φ (x) на функцію ψ (x) так, що їх значення співпадають в заданих точках φ (xi) = ψ (xi), i = 1, 2…, n називають інтерполяцією.
Проте таке вирішення проблеми не є задовільним, оскільки yi ≠ φ (xi) із-за випадкових помилок вимірювання і впливу на вимірювання значень yі перешкод і шумів в пристрої. Отже yi = φ (xi)+δ i, де δ i - деяка випадкова помилка. Тому потрібно провести криву так, щоб вона в найменшій мірі залежала від випадкових помилок. Це завдання називається згладжуванням (апроксимацією) експериментальної залежності і часто вирішується методом найменших квадратів. Згладжуючу криву називають апроксимуючою.
Завдання апроксимації вирішується таким чином. У декартовій прямокутній системі координат наносять точки (xi, yi). По розташуванню цих точок робиться припущення про приналежність шуканої функції до певного класу функцій. Наприклад, лінійна функція φ (x)= α 0 +α 1 x, квадратична φ (x)=α 0+α 1x+ α 2x2, і так далі У загальному випадку (x)= φ (x, α 0, α 1, α 2, …, α r). Невідомі параметри функції α 0, α 1, α 2, …, α r визначаються з вимоги мінімуму суми квадратів випадкових помилок, тобто мінімуму величини
δ =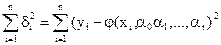 
Величина δ називається також сумарною нев'язністю. Необхідною умовою мінімуму функції декілька змінних є перетворення на нуль частинних похідних нев'язності:
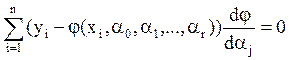, j = 0, 1, …r 
Розв’язуючи систему рівнянь, знаходимо невідомі параметри α j і тим самим повністю визначаємо функцію, яка найкращим чином (у сенсі найменших квадратів відхилень від початкових точок або найменшої сумарної нев'язності) апроксимує (наближає) шукану функцію φ (x).
Зупинимося докладніше на лінійній залежності φ (x)= α 0 +α 1 x.
Диференціюючи, отримаємо наступну систему рівнянь:
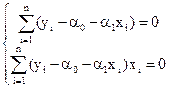
З першого рівняння знаходимо α 0 = М y –α 1M x, де
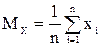
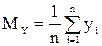
Підставляючи вираз для α 0 у друге рівняння, знайдемо
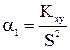
де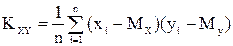 
, 
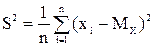
Таким чином,
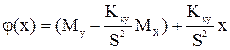
є шукана лінійна функція.
Зважаючи на простоту розрахунків апроксимація лінійної залежності використовується досить часто. Крім того, багато функцій, залежних від двох параметрів, можна лінеарізувати шляхом заміни змінних.
Для цього необхідно підібрати таке перетворення початкової залежності y (x)= φ (x, α 0, α 1), в результаті якого вона набуває лінійного вигляду y = b 0 +b 1 u. Далі розв’язується завдання лінійної апроксимації для нової залежності і обчислені коефіцієнти b 0 і b 1 перераховуються в коефіцієнти α 0 і α 1.