
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методы проецирования
|
|
ОГЛАВЛЕНИЕ
1. МЕТОДЫ ПРОЕЦИРОВАНИЯ …………………………………………………………………………5
1.1.Центральное проецирование………………………………………………………...5
1.2.Параллельное и ортогональное проецирование……………………………………5
1.3.Свойства ортогонального проецирования………………………………………….5
1.4.Обратимость чертежа………………………………………………………………...6
2. ТРЁХКАРТИННЫЙ ЧЕРТЕЖ ТОЧКИ ……………………………………………………...7
2.1.Аппарат проецирования……………………………………………………………..7
2.2.Конкурирующие точки……………………………………………………………….8
3. ЧЕРТЕЖ ПРЯМОЙ ………………………………………………………………………...9
3.1.Положение прямой относительно плоскостей проекций…………………………9
3.1.1.Прямая общего положения………………………………………………………9
3.1.2.Прямая уровня…………………………………………………………………..10
3.1.3.Проецирующая прямая…………………………………………………………11
3.2.Взаимное положение прямых……………………………………………………...11
4. КОМПЛЕКСНЫЙ ЧЕРТЕЖ ПЛОСКОСТИ..........................................................................11
4.1.Положение плоскости относительно плоскостей проекций…………………….12
4.1.1.Плоскость общего положения………………………………………………….12
4.1.2.Проецирующая плоскость………………………………………………………12
4.1.3.Плоскость уровня………………………………………………………………..13
4.2.Принадлежность прямой и точки плоскости……………………………………...13
4.3.Прямые особого положении в плоскости………………………………………….14
4.3.1.Прямая уровня плоскости…………………………………………....................14
4.3.2. Прямая наибольшего наклона плоскости
к какой-либо плоскости проекций…………………………………………….15
5. ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ, ДВУХ ПЛОСКОСТЕЙ …………..16
5.1.Параллельность прямой и плоскости……………………………………………...16
5.2.Параллельность плоскостей………………………………………………………..16
5.3.Пересечение прямой и плоскости………………………………………………….16
5.3.1.Пересечение прямой и плоскости частного положения……………………...16
5.3.2.Пересечение плоскостей, одна из которых –
частного положения……………………………………………………………...17
5.3.3. Пересечение прямой и плоскости общего положения
(первая основная позиционная задача)……………………………………………17
5.4.Пересечение плоскостей общего положения
(вторая основная позиционная задача)…………………………………………...18
5.5.Перпендикулярность прямых и плоскостей………………………………………19
5.5.1.Перпендикуляр к плоскости……………………………………………………19
5.5.2.Плоскость, перпендикулярная прямой………………………………………...20
5.5.3.Взаимно перпендикулярные прямые…………………………………………..20
5.5.4.Взаимно перпендикулярные плоскости………………………………………20
6. СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА ……………………………………………...21
6.1.Замена плоскостей проекций………………………………………………………21
6.2.Плоскопараллельное перемещение………………………………………………..23
6.3.Вращение вокруг проецирующей прямой………………………………………...25
6.4.Вращение вокруг прямой уровня………………………………………………….25
7. МНОГОГРАННИКИ ………………………………………………………………………27
7.1.Пересечение многогранника плоскостью…………………………………………27
7.2.Пересечение многогранника прямой………………………………………………29
7.3.Взаимное пересечение многогранников…………………………………………...30
8. КРИВЫЕ ЛИНИИ ………………………………………………………………………….32
8.1.Плоские кривые. Касательные и нормали………………………………………….32
8.2.Основные свойства проекций плоских кривых линий…………………………….33
8.3.Проецирование окружности…………………………………………………………33
8.4.Цилиндрическая винтовая линия……………………………………………………35
9. КРИВОЛИНЕЙНЫЕ ПОВЕРХНОСТИ ……………………………………………………...36
9.1.Очерк поверхности…………………………………………………………………..36
10. ПОВЕРХНОСТИ ВРАЩЕНИЯ ……………………………………………………………..37
10.1.Основные линии поверхности вращения………………………………………….37
10.2.Пересечение криволинейной поверхности плоскостью………………………….39
10.2.1.Cферические сечения…………………………………………………………...39
10.2.2.Цилиндрические сечения……………………………………………………….39
10.2.3.Конические сечения…………………………………………………………….39
10.3.Построение сечения поверхности вращения плоскостью………………………..40
10.4.Пересечение поверхности прямой линией………………………………………..41
11. ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ …………………………………………42
11.1.Пересечение криволинейной и гранной поверхностей…………………………..42
11.2.Пересечение поверхностей вращения второго порядка………………………….44
11.2.1.Способ секущих плоскостей……………………...............................................44
11.2.2.Способ концентрических секущих сфер………………………………………46
11.3.Особые случаи пересечения поверхностей вращения второго порядка……..48
12. РАЗВЕРТКИ ПОВЕРХНОСТЕЙ ……………………………………………………………49
12.1.Развертка призмы……………………………………………………………………49
12.2.Развертка пирамиды………………………………………………………………...52
12.3. Развертка цилиндрической поверхности……….....................................................53
12.4. Развертка конической поверхности…………………………………….................54
13. ЛИТЕРАТУРА ……………………………………………………………………………..56
МЕТОДЫ ПРОЕЦИРОВАНИЯ
Для построения чертежа применяются различные методы проецирования.
1.1.Центральное проецирование
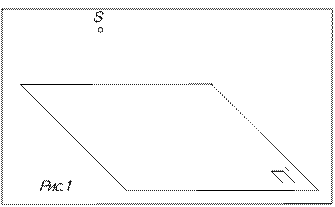
В аппарат центрального прое-цирования (параметры, выбираемые проектировщиком) входят:
- плоскость проекций П',
- центр проекций S.
 Чтобы построить центральную проекцию точки А пространства, нужно через центр S и точку А провести прямую, называемую проецирующей. Точка пересечения проецирующей прямой с плоскостью проекций и будет центральной проекцией А' точки А.
Чтобы построить центральную проекцию точки А пространства, нужно через центр S и точку А провести прямую, называемую проецирующей. Точка пересечения проецирующей прямой с плоскостью проекций и будет центральной проекцией А' точки А.
1.2.Параллельное и ортогональное проецирование
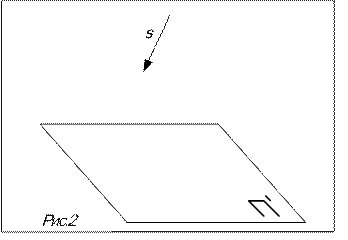
Аппарат параллельного проецирования:
- плоскость проекций П',
- направление проецирования s.
Чтобы построить параллельную про-екцию точки А пространства, нужно через точку А провести проецирующую прямую, параллельную s. Точка пересе-чения проецирующей прямой с плос-костью проекций и будет паралл е ль-ной проекцией А' точки А.
Если направление проецирова-ния перпендикулярно плоскости проек-ций, то такое проецирование называется ортогональным.
1.3.Свойства ортогонального проецирования
1.  Проекцией точки является точка (рис.2.)
Проекцией точки является точка (рис.2.)
2. Проекцией прямой, не перпендикулярной плоскости проекций, является прямая, а прямой, перпендикулярной плоскости проекций – точка (рис.3).
3. Если точка принадлежит прямой, то проекция точки принадлежит проекции прямой (рис.3).
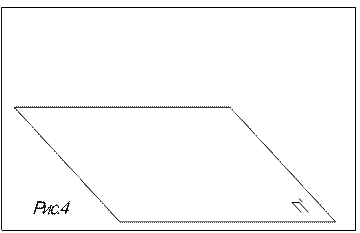
4. Если прямые параллельны, то их проекции параллельны или совпадают (рис.4).
5.  Отношение отрезков, лежащих на одной прямой или на параллельных прямых, равно отношению проекций этих отрезков: [ АС ]: [ ВС ] = [ A'C' ]: [ В'С' ] (рис.3.)
Отношение отрезков, лежащих на одной прямой или на параллельных прямых, равно отношению проекций этих отрезков: [ АС ]: [ ВС ] = [ A'C' ]: [ В'С' ] (рис.3.)
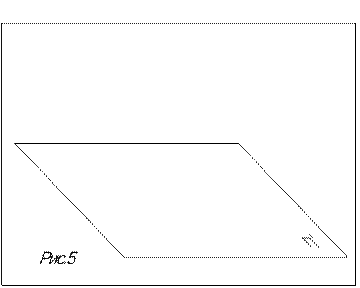 6. Длина проекции отрезка, наклонного к плоскости проекций, меньше длины отрезка в пространстве и равна [ A/B/ ] = [ AB ]× Cos α (рис.5), что следует из треугольника АВА*.
6. Длина проекции отрезка, наклонного к плоскости проекций, меньше длины отрезка в пространстве и равна [ A/B/ ] = [ AB ]× Cos α (рис.5), что следует из треугольника АВА*.
7.Если одна сторона прямого угла па-раллельна плоскости проекций, а другaя к ней не перпендикулярна, то прямой угол проецируется в натуральную величину (рис.6):
если прямая перпендикулярна двум пересекающимся прямым плоскости å, то она перпендикулярна этой плоскости и любой прямой ей принадлежащей:
 (АВ)^(ВС) и (АВ)^(ВВ/), то (АВ)^ S.
(АВ)^(ВС) и (АВ)^(ВВ/), то (АВ)^ S.
(А/В/)║ (АВ), следовательно(А/В/)^ S и (В/С/)^.(А/В/)
8. Проекция фигуры не изменяется при параллельном переносе плоскости проекций.
31.4.Обратимость чертежа
Проекции точки А' (рис.2) соответствует бесконечное множество точек А в простран-стве, расположенных на проецирующей прямой АА', т.е. реконструировать однозначно точку в пространстве невозможно и такой чертеж не обладает свойством обратимости. Впервые задачу создания обратимого (комплексного) чертежа решил французский учёный Гаспар Монж, предложивший ортогонально проецировать точку на две и более взаимно перпендикулярных плоскости проекций. Стандартом Единой системы конструкторской документации (ЕСКД) установлено 6 основных плоскостей проекций, образующих грани куба.