
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Взаимное положение прямой и плоскости, двух плоскостей
|
|
5.1.Параллельность прямой и плоскости
Определение: прямая и плоскость называются параллельными, если они не имеют общей точки.
Признак: прямая параллельна плоскости, если она параллельна прямой, лежащей в плоскости.
Задача. Через точку М провести прямую l, параллельную плоскости D (a  b) и П1 (рис.33).
b) и П1 (рис.33).
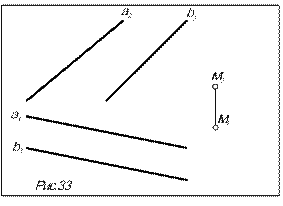 Алгоритм решения
Алгоритм решения
1. Т.к. искомая прямая l должна быть параллельна П1, в плоскости D (a  b) проводим произвольную горизонталь h: сначала h2
b) проводим произвольную горизонталь h: сначала h2  x12, а затем h1 по точкам 1 и 2: 11
x12, а затем h1 по точкам 1 и 2: 11 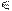 h1
h1 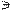 21
21
2. Через проекции точки М проводим l2  h2 и l1
h2 и l1  h1.
h1.
Задача решена: прямая l  D (a
D (a  b), т.к. она параллельна h, лежащей в плоскости, и l
b), т.к. она параллельна h, лежащей в плоскости, и l  П1, т.к. l2
П1, т.к. l2  x12.
x12.
5.2.Параллельность плоскостей
Определение: плоскости являются параллельными, если не имеют общей точки.
Признак: если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны
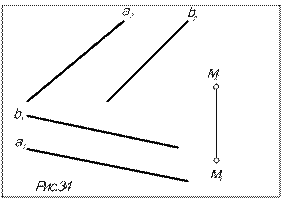 Задача. Через точку М провести плоскость S, параллельную плоскости D (a
Задача. Через точку М провести плоскость S, параллельную плоскости D (a  b) (рис.34).
b) (рис.34).
Алгоритм решения
1. В заданной плоскости нет пересекающихся прямых, поэтому проводим в ней дополнительную прямую с, пересекающую прямые, задающие плоскость D (a  b).
b).
2. Искомую плоскость S задаём двумя пересекающимися прямыми m  a и l
a и l  с, проведенными через точку М.
с, проведенными через точку М.
5.3.Пересечение прямой и плоскости
5.3.1.Пересечение прямой и плоскости частного положения
Задача. Построить точку К пересечения прямой l с проецирующей плоскостью S (рис.35).
Алгоритм решения
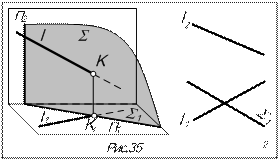 Точка К общая для прямой и плоскости. Из условия принадлежности её плоскости S горизонтальная проекция К1 должна располагаться на вырожденной проекции плоскости S1. Из условия принадлежности её прямой l проекции точки должны лежать на проекциях прямой. Следовательно, К1 лежит в точке пересечения S1 и l1: l1
Точка К общая для прямой и плоскости. Из условия принадлежности её плоскости S горизонтальная проекция К1 должна располагаться на вырожденной проекции плоскости S1. Из условия принадлежности её прямой l проекции точки должны лежать на проекциях прямой. Следовательно, К1 лежит в точке пересечения S1 и l1: l1 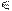 К1
К1 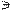 S1. Фронтальная проекция К2 находится по принадлежности прямой l: К2 Î l2.
S1. Фронтальная проекция К2 находится по принадлежности прямой l: К2 Î l2.
Видимость прямой на П2 определяем «по представлению»: рассматриваем горизонтальную проекцию совместно с направлением взгляда наблюдателя на П2 и видим, что при взгляде на П2 часть прямой правее точки К располагается за плоскостью S и является невидимой.
 5.3.2.Пересечение плоскостей, одна из которых – частного положения
5.3.2.Пересечение плоскостей, одна из которых – частного положения
Задача. Построить линию пересечения m двух плоскостей, одна из которых - проецирующая (рис.36).
Алгоритм решения
1. Линия пересечения принадлежит фронтально проецирующей плоскости, следовательно, фронтальная проекция линии совпадает с вырожденной проекцией плоскости: m2 = S2.
2. Линия пересечения m принадлежит плоскости треугольника АВС, следовательно, она пересекает стороны треугольника АВ и АС в точках 1 и 2. Построив горизонтальные проекции этих точек по принадлежности сторонам треугольника и соединив их, получаем горизонтальную проекцию искомой линии пересечения m1.
 3. Видимость треугольника на П1 определяем так же, как и в предыдущей задаче, «по представлению»: рассматриваем фронтальную проекцию совместно с направлением взгляда наблюдателя на П1 и видим, что при взгляде сверху часть треугольника (А12) располагается ниже плоскости S и является невидимой.
3. Видимость треугольника на П1 определяем так же, как и в предыдущей задаче, «по представлению»: рассматриваем фронтальную проекцию совместно с направлением взгляда наблюдателя на П1 и видим, что при взгляде сверху часть треугольника (А12) располагается ниже плоскости S и является невидимой.
5.3.3. Пересечение прямой и плоскости общего положения
(п ервая основная позиционная задача)
Алгоритм решения(рис.37)
1. Через заданную прямую l проводится проецирующая плоскость S.
2. Строится линия m пересечения плоскостей D и S.
3. Находится точка К пересечения прямой l с построенной линией пересечения m: l 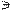 К
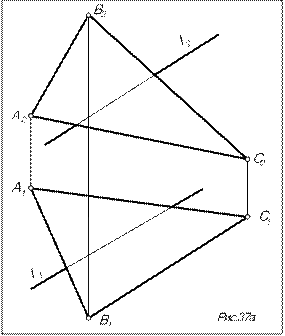
К 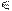 m. Это и есть искомая точка пересечения прямой l с плоскостью.
m. Это и есть искомая точка пересечения прямой l с плоскостью.
 Задача. Построить точку К пересечения прямой l с плоскостью q (DАВС) (рис.37а).
Задача. Построить точку К пересечения прямой l с плоскостью q (DАВС) (рис.37а).
Т.к. заданные прямая и плоскость – об-щего положения, то применяем алгоритм ре-шения первой основной позиционной задачи.
1. Прямую l заключаем во фронтально проецирующую плоскость S: l2 = S2.
2. Строим линию пересечения m плоскостей q и S:
2.1. Фронтальную проекцию m находим из условия её принадлежности плоскости S: m Î S Þ m2 =S2 ,
2.2. Горизонтальную проекцию m находим из условия её принадлежности плоскости q: m пересекает стороны ВС и АС:
m Î q Þ m  ВС =1, m
ВС =1, m  АС =2.
АС =2.
Фронтальные проекции точек 1 и 2 находим как результат пересечения одноименных проекций m, ВС и АС:
12 = m2  В2С2, 22 = m2
В2С2, 22 = m2  А2С2 , а горизонтальные – по принадлежности сторонам треугольника: 11Î В1С1, 21Î А1С1 . Соединив горизонтальные проекции точек 1 и 2, получим горизонтальную проекцию линии пересечения: 11
А2С2 , а горизонтальные – по принадлежности сторонам треугольника: 11Î В1С1, 21Î А1С1 . Соединив горизонтальные проекции точек 1 и 2, получим горизонтальную проекцию линии пересечения: 11 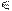 m1
m1 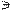 21.
21.
3. Находим точку пересечения прямой l с треугольником АВС: К1= m1  l1, К2Î l2.
l1, К2Î l2.
4. Видимость прямой определяем с помощью конкурирующих точек. На прямой l берем точку 3, фронтально конкурирующую с точкой 1, по построению принадлежащей стороне ВС треугольника. Рассматриваем горизонтальную проекцию совместно с направлением взгляда на П2. Точка 1 (треугольник) ближе к наблюдателю и заслоняет точку 3 (прямую l), следовательно, правее точки К (граница видимости) прямая l является невидимой. На П1 видимость можно определить аналогичным образом, но проще воспользоваться тем, что плоскость q (D АВС) – нисходящая, и у неё на П1 и П2 видны разные стороны, а следовательно, и разные участки прямой l: на горизонтальной проекции невидимым является участок левее точки К.
5.4.Пересечение плоскостей общего положения (вторая основная позиционная задача
Алгоритм построения линии пересечения
Для построения линии пересечения плоскостей общего положения применяется метод вспомогательных секущих плоскостей(рис.38):
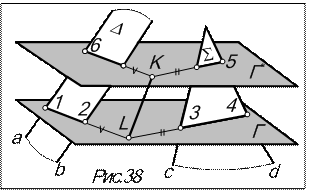 1.Проводится вспомогательная проецирующая плоскость Г, пересекающая заданные (D (а
1.Проводится вспомогательная проецирующая плоскость Г, пересекающая заданные (D (а  в) и S (c
в) и S (c  d)).
d)).
2.Строятся линии пересечения вспомо-гательной плоскости с заданными:
(12) = Г  D(а
D(а  в), (34) = Г
в), (34) = Г  S (c
S (c  d).
d).
3.Находится точка пересечения построенных линий пересечения: L= (12)  (34). Эта точка – общая для двух заданных плоскостей и, следовательно, лежит на линии их пересечения.
(34). Эта точка – общая для двух заданных плоскостей и, следовательно, лежит на линии их пересечения.
4. Введя еще одну вспомогательную проецирующую плоскость Г*, по аналогичному алгоритму находим вторую точку линии пересечения К. Если Г  Г*, то построение линии пересечения вспомогательной плоскости Г* с заданными значительно упрощается, т.к. параллельными плоскостями плоскость пересекается по параллельным прямым.
Г*, то построение линии пересечения вспомогательной плоскости Г* с заданными значительно упрощается, т.к. параллельными плоскостями плоскость пересекается по параллельным прямым.
5. Соединив одноименные проекции точек L и К, находим линию пересечения заданных плоскостей
Задача. Построить линию пересечения плоскостей общего положения D (а  в) и
в) и
S (c  d ) (рис.38а).
d ) (рис.38а).
 Алгоритм решения
Алгоритм решения
1.Проводим горизонтальную плоскость Г, пересекающую заданные плоскости.
2.Строим линии m и n пересечения вспомогательной плоскости Г с заданными плоскостями D(а  в) и S(c
в) и S(c  d).
d).
Фронтальные их проекциинаходим из ус-ловия принадлежности линий пересечения плоскости Г: m2 = n2 = Г2. Горизонтальные проекции линий пересечения находим из условия их принадлежности плоскостям D (а  в) и S (c
в) и S (c  d): располагаясь в D и S, прямые m и n пересекают прямые, задающие эти плоскости в точках 1, 2, 3, 4 соответственно. Найдя фронтальные проекции этих точек как результат пересечения одноименных проекций прямых: 12 = a2
d): располагаясь в D и S, прямые m и n пересекают прямые, задающие эти плоскости в точках 1, 2, 3, 4 соответственно. Найдя фронтальные проекции этих точек как результат пересечения одноименных проекций прямых: 12 = a2  m2 , 22 = b2
m2 , 22 = b2  m2, 32 = с2
m2, 32 = с2  n2, 42 = d2
n2, 42 = d2  n2, горизонтальные их проекции находим по принадлежности соответствующим прямым: 11Î a1, 21 Î b1, 31Î с1, 41Î d1. Соединив попарно точки 11, 21 и 31, 41, получим горизонтальные проекции m1 и n1 .
n2, горизонтальные их проекции находим по принадлежности соответствующим прямым: 11Î a1, 21 Î b1, 31Î с1, 41Î d1. Соединив попарно точки 11, 21 и 31, 41, получим горизонтальные проекции m1 и n1 .
3. Находим точку К – общую для заданных плоскостей: К1 = m1  n1 и К2Î Г2
n1 и К2Î Г2
4. Вторую точку L искомой линии пересечения заданных плоскостей находим по аналогичному алгоритму, проведя вспомогательную плоскость Г*  Г.
Г.
5. Соединив одноименные проекции точек L и К, находим линию пересечения заданных плоскостей
5.5.Перпендикулярность прямых и плоскостей
5.5.1.Перпендикуляр к плоскости
 Если плоскость – частного положения, то перпендикуляр к ней тоже прямая частного положения: перпендикуляр к проецирующей плоскости – линия уровня, к плоскости уровня – проецирующая прямая (рис.39). Проведение нормали к плоскости не требует каких-либо построений.
Если плоскость – частного положения, то перпендикуляр к ней тоже прямая частного положения: перпендикуляр к проецирующей плоскости – линия уровня, к плоскости уровня – проецирующая прямая (рис.39). Проведение нормали к плоскости не требует каких-либо построений.
Если плоскость – общего положения, то перпендикуляр к ней тоже прямая общего положения и его построение основывается на следующем положении.
Определение: прямая перпендикулярна плоскости, если она перпендикулярна к каждой из двух пересекающихся прямых, лежащих в плоскости. Если пересекающиеся прямые – линии уровня плоскости, то по теореме проецирования прямого угла в горизонтальную плоскость проекций проецируется в натуральную величину прямой угол между перпендикуляром n и горизонталью, а во фронтальную - прямой угол между перпендикуляром и фронталью: n1 ^ h1 и n2 ^ f2.
Задача. Из точки D опустить перпендикуляр на плоскость S (D АВС) и найти его основание (рис.40).
Алгоритм решения
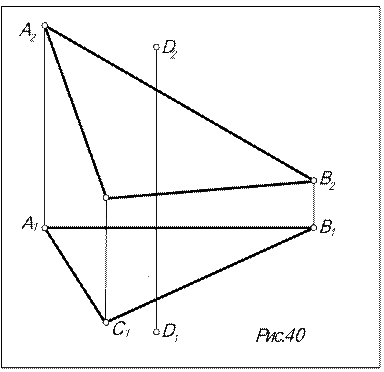 1. Проводим в плоскости S произвольные линии уровня.
1. Проводим в плоскости S произвольные линии уровня.
Фронталь плоскости уже имеет-ся – сторона АВ. Горизонталь h проводим через вершину В: В2Î h2  x2, В1
x2, В1 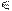 h1
h1 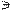 11.
11.
2. Через точку D проводим нормаль к плоскости: D1 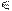 n1 ^ h1, D2
n1 ^ h1, D2 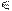 n2 ^ f2.
n2 ^ f2.
3. Находим основание перпендикуляра (первая основная позиционная задача):
3а. Заключаем нормаль во фронтально проецирующую плоскость Q: Q2 = n2.
3б. Строим линию l пересечения плоскостей Q и S (D АВС): l Ì Q Þ l2 = Q2;