
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Комплексный чертеж плоскости
|
|
Плоскость считается заданной на чертеже, если:
-возможно построить проекции любой точки, принадлежащей плоскости;
-возможно определить, принадлежит ли данной плоскости заданная на чертеже точка.
В общем случае плоскость задается на чертеже проекциями своего определителя, под которым понимается совокупность элементов, однозначно задающих плоскость в пространстве (рис.22): три точки, не лежащие на одной прямой, прямая и точка вне прямой, две пересекающие прямые, две параллельные прямые, плоская фигура.
 4.1.Положение плоскости относительно плоскостей проекций
4.1.Положение плоскости относительно плоскостей проекций
4.1.1.Плоскость общего положения
Определение: плоскость, наклоненная ко всем плоскостям проекций (рис.23).
Признак: ни на одну из плоскостей проекций определитель плоскости не проецируется на прямую (см. рис.22).
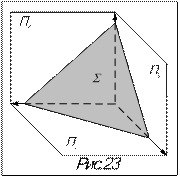 Свойства чертежа: фигура в плоскости общего положения, углы наклона её к плоскостям проекций ни на одну плоскость проекций не проецируется в натуральную величину.
Свойства чертежа: фигура в плоскости общего положения, углы наклона её к плоскостям проекций ни на одну плоскость проекций не проецируется в натуральную величину.
Восходящей называется плоскость, высота точек которой возрастает по мере удаления от наблюдателя, а нисходящей - плоскость, высота точек которой уменьшается по мере удаления от наблюдателя. Признак: у восходящей плоскости обход проекцийточек на обеих плоскостях проекций одинаковый (плоскости L и q на рис.22), у нисходящей – противоположный (плоскость S на рис.22). У восходящей плоскости видна на П1 и П2 одна и та же сторона, у нисходящей - разные стороны.
4.1.2. Проецирующая плоскость
Определение: плоскость, перпендикулярная какой-либо плоскости проекций (рис.24). 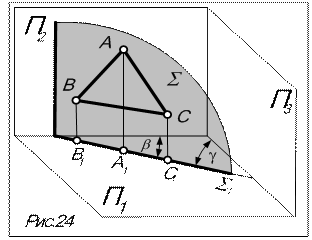

Признак: проекция плоскости на перпендикулярную плоскость проекций – прямая (вырожденная проекция плоскости), наклоненная к осям проекций (S на рис.24, 25). На комплексном чертеже проецирующие плоскости задаются, как правило, своими вырожденными проекциями (см. рис.25).
Свойства чертежа: вырожденная проекция обладает собирательным свойством: проекция фигуры, расположенной в плоскости, в перпендикулярную плоскость проекций располагается на вырожденной проекции проецирующей плоскости. Углы наклона вырожденной проекции к осям проекций равны углам наклона плоскости к соответствующим плоскостям проекций.
В зависимости от плоскости проекций, к которой перпендикулярна плоскость, проецирующие плоскости называются горизонтально, фронтально или профильно проецирующими.
4.1.3.Плоскость уровня

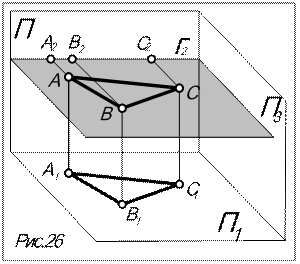 Определение: плоскость, параллельная какой-либо плоскости проекций (рис.26).
Определение: плоскость, параллельная какой-либо плоскости проекций (рис.26).
Признак: проекция плоскости на перпендикулярную плоскость проекций – прямая (вырожденная проекция) Г2, параллельная осям проекций (рис.27).
Свойства чертежа: фигура в плоскости уровня в параллельную плоскость проекций проецируется в натуральную величину.
4.2.Принадлежность прямой и точки плоскости
Прямая принадлежит плоскости:
а) если прямая проходит через две точки, принадлежащие плоскости;
б) если прямая проходит через точку плоскости и параллельна прямой, лежащей в плоскости.
 Точка принадлежит плоскости, если она лежит на прямой, принадлежащей плоскости.
Точка принадлежит плоскости, если она лежит на прямой, принадлежащей плоскости.
Задача. Построить недостающую проекцию точки А, принадлежащей плоскости S (m  n) (рис.28).
n) (рис.28).
Алгоритм решения
1. Через известную горизонтальную А1 проекцию точки А проводим проекцию произвольной пря-мой l так, чтобы она пересекала прямые m и n, за-дающие плоскость S: А1 Î l1
2. Находим проекции точек 1 и 2 пересечения прямой l с прямыми m и n:
11 = l1  m1, 21 = l1
m1, 21 = l1  n1 , 12 Î m2 , 22 Î n2 .
n1 , 12 Î m2 , 22 Î n2 .
3. Соединив 12 и 22 , получаем фронтальную l2 проекцию прямой l, по принадлежности которой и находим фронтальную проекцию точки А: А2 Î l 2.
4.3.Прямые особого положении в плоскости
4.3.1.Прямая уровня плоскости
Определение: прямая, принадлежащая плоскости и параллельная какой-либо плоскости проекций.
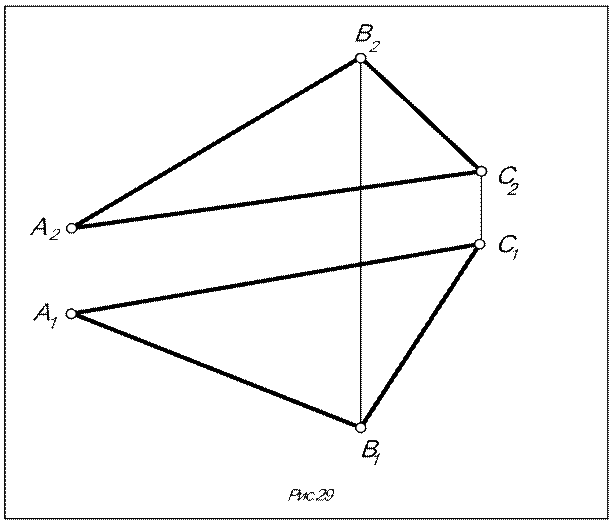 Задача. В плоскости q (D АВС) провести произвольные горизонталь и фронталь (рис 29).
Задача. В плоскости q (D АВС) провести произвольные горизонталь и фронталь (рис 29).
Алгоритм решения
1.Т.к. требуется построить произвольные горизонталь и фронталь, то для удобства построений проведем их соответственно через вершины С и А треугольника.
2. Сначала проводим те проекции прямых, направление которых известны – фронтальную проекцию горизонтали h2 и горизонтальную фронтали f1: C2 Î h2  X12, А1 Î f1
X12, А1 Î f1  X12 .
X12 .
 3. Недостающие проекции прямых находим по принадлежности их плоскости треугольника АВС, а именно по двум точкам ей принадлежащим. Для этого находим точки 1 и 2 пересечения горизонтали и фронтали со сторонами АВ и ВС соответственно и соединяем их с одноименными проекциями А и С.
3. Недостающие проекции прямых находим по принадлежности их плоскости треугольника АВС, а именно по двум точкам ей принадлежащим. Для этого находим точки 1 и 2 пересечения горизонтали и фронтали со сторонами АВ и ВС соответственно и соединяем их с одноименными проекциями А и С.
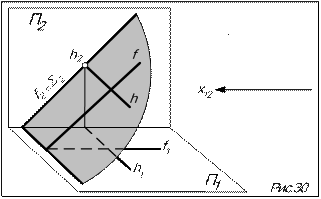
В проецирующей плоскости пря-мая уровня, параллельная неперпендику-лярной плоскости проекций – прое-цирующая прямая (рис.30).
4.3.2.Прямая наибольшего наклона плоскости к какой-либо плоскости проекций
 Определение: прямая, лежащая в плоскости, и перпендикулярная соответствующей линии уровня плоскости.
Определение: прямая, лежащая в плоскости, и перпендикулярная соответствующей линии уровня плоскости.
Признак: в плоскость проекций, параллельную линии уровня, прямой угол между линией наибольшего на-клона и линией уровня проецируется в натуральную величину.
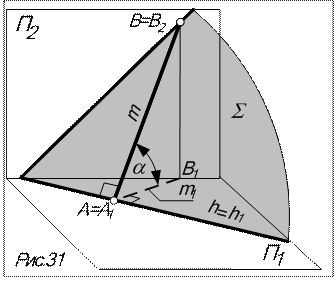
Прямая наибольшего наклона используется для определения вели-чины двугранного угла между плос-костью общего положения и какой-либо плоскостью проекций: двугран-ный угол измеряется линейным углом между линией наибольшего наклона плоскости и ее проекцией на соответствующую плоскость проекций.
На рис.31 показана прямая наибольшего наклона m плоскости å к горизонтальной плоскости проекций (линия ската), проведенная перпендикулярно горизонтали h. При этом m1 ^ h 1. Угол a между линией ската m и её проекцией m1 и есть угол между плоскостями å и П1 .
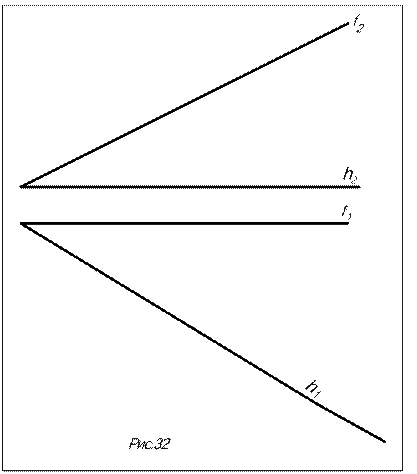 Задача. Определить углы наклона плоскости S (f
Задача. Определить углы наклона плоскости S (f  h) к плоскостям проекций П1 и П2 (рис.32).
h) к плоскостям проекций П1 и П2 (рис.32).
Алгоритм решения
1.Определение угланаклона å к П1 .
1.1.Проводим произволь-ную линию ската m: сначала её горизонтальную проекцию m1 ^ h1, а затем, по двум то-чкам 1 и 2 пересечения линии ската с горизонталью и фрон-талью плоскости, её фронта-льную проекцию 12 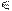 m2
m2 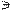 22. 1.2. Строим прямоугольный треугольник для определения натуральной величины отрезка (12): в качестве первого катета берём горизонтальную проекцию отрезка (1121), а в качестве второго – разность высот Dh точек 1 и 2. Угол между натуральной величиной (2110) отрезка и его проекцией (1121) и есть искомый угол a наклона плоскости å к П1
22. 1.2. Строим прямоугольный треугольник для определения натуральной величины отрезка (12): в качестве первого катета берём горизонтальную проекцию отрезка (1121), а в качестве второго – разность высот Dh точек 1 и 2. Угол между натуральной величиной (2110) отрезка и его проекцией (1121) и есть искомый угол a наклона плоскости å к П1
2. По аналогичному алгоритму, проведя линию n наибольшего наклона плоскости å к П2, находим угол b.