
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Развертки поверхностей
|
|
Разверткой называется фигура, полученная совмещением с плоскостью без складок и разрывов гранной или криволинейной поверхности, которые можно представить себе как гибкую нерастяжимую пленку. Не все поверхности являются развертываемыми. К последним относятся гранные поверхности, цилиндр, конус и торс, а все остальные криволинейной поверхности можно развернуть только приближенно, заменяя (аппроксимируя) развертывающимися поверхностями.
12.1.Развертка призмы
Развертка призмы представляет собой фигуру, состоящую из натуральной величины боковых граней и обоих оснований. Мысленно разрезав многогранник по одному из боковых ребер и ребрам оснований, вращением вокруг остальных ребер последовательно совмещаем все грани с плоскостью проекций.
Для построения развертки призмы необходимо знать натуральные величины ребер призмы и нормального сечения. Нормальным называется сечение призмы плоскостью, перпендикулярной боковым ребрам. При развертывании боковой поверхности призмы нормальное сечение разворачивается в прямую, перпендикулярную проекциям боковых ребер на развертке.
Задача. Построить развертку прямой треугольной усеченной призмы (рис.88).
Т.к. призма прямая, то основание ее будет нормальным сечением, которое на П1 проецируется в натуральную величину. Ребра призмы - фронтальные прямые, следовательно,
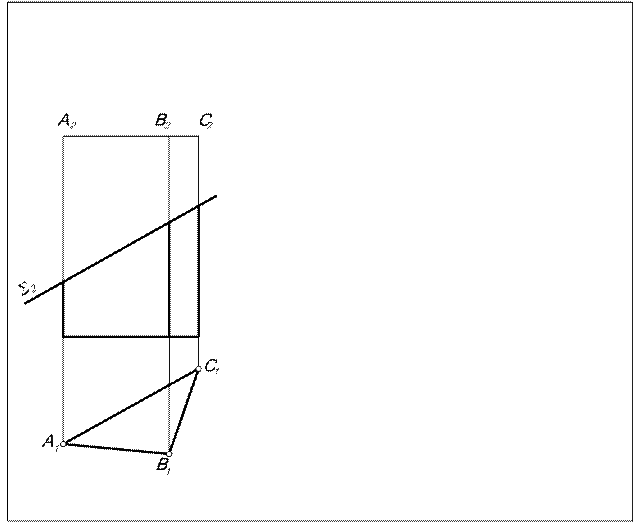 на П2 они проецируются в натуральную величину. Таким образом, все необходимые данные для построения развертки уже имеются на чертеже.
на П2 они проецируются в натуральную величину. Таким образом, все необходимые данные для построения развертки уже имеются на чертеже.
Алгоритм построения развертки:
1. Строим развертку боковой поверхности усеченной призмы.
На свободном поле чертежа (для удобства построений – в проекционной связи с фрон-тальной проекцией нижнего основания) строим развертку нормального сечения (основания) – проводим прямую, на которой откладываем НВ ребер основания, взяв их с горизонтальной проекции – [ АВ ] = [ А1В1 ] и т.д.
Через построенные на развертке вершины основания проводим прямые, перпендикуляр-ные развертке основания, и откладываем на них НВ боковых ребер и отрезков, отсекаемых на них секущей плоскостью S; если развертка строится в проекционной связи с фронталь-ной проекцией призмы (как на рис.87), то для этого достаточно провести горизонтальные линии связи до пересечения с проекциями соответствующих ребер.
2. Пристраиваем к полученной развертке боковой поверхности НВ основания и сечения, строя их по их трем известным сторонам (методом триангуляции). Для построения НВ сечения выбираем в качестве исходной его сторону (23), и из точек 2 и 3 проводим дуги окружностей, радиусы которых равны соответственно [ 12 ] и [ 13 ]. Точка пересечения этих дуг и есть вершина А сечения. Аналогично строим НВ основания.
Задача. Построить развертку боковой поверхности наклонной призмы (рис.89).
Боковые ребра и нормальное сечение призмы занимают общее положение и проецируются на плоскости проекций с искажением, поэтому, прежде чем приступать к построению развертки, необходимо определить их натуральные величины. 
Алгоритм решения
1. Определяем НВ боковых ребер методом замены плоскостей проекций, проводя вместо П2 дополнительную плоскость проекций П4, параллельную боковым ребрам:
: П2 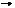 П4
П4  АD, П1 / П2 (x12)
АD, П1 / П2 (x12) 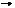 П1 / П4 (s14
П1 / П4 (s14  А1D1). Строим проекцию призмы в П4 по известному алгоритму (см. стр.21, рис.43). Проекции боковых ребер в П4 являются их НВ.
А1D1). Строим проекцию призмы в П4 по известному алгоритму (см. стр.21, рис.43). Проекции боковых ребер в П4 являются их НВ.
2. Определяем НВ нормального сечения. Проводим в системе П1 / П4 плоскость нормального сечения S, перпендикулярную боковым ребрам. Т.к. последние параллельны П4, то прямой угол между S и боковыми ребрами проецируется в П4 в НВ: S4 ^ A4D4. Строим проекции нормального сечения сначала в П4 (отрезок 142434), а затем в П1, находя вершины сечения по принадлежности соответствующим ребрам. НВ нормального сечения находим методом плоско параллельного перемещения относительно П4, выставляя при этом сечение параллельно П1 , а его проекцию параллельно оси s14. Величина проекции на П4 при этом не изменяется: [ 142434 ] = [ 14*24*34* ]. Строим проекцию нормального сечения на П1, находя проекции его вершин 11*, 21*, 31* как результат пересечения траекторий перемещения проекций вершин на П1 с соответствующими линиями связи в системе П1 / П4. Треугольник (11*21*31*) и будет НВ нормального сечения.
3. Строим развертку боковой поверхности призмы. На свободном поле чертежа проводим прямую и строим на ней развертку нормального сечения, откладывая на ней НВ ребер нормального сечения: [ 12 ] = [ 11*21* ] и т.д. Через построенные точки 1, 2, 3, 1 проводим прямые, перпендикулярные развертке нормального сечения – проекции боковых ребер на развертке, и откладываем на них НВ отрезков, на которые делит ребра плоскость S, беря их с проекции призмы на П4: [ A1 ] = [ A414 ], [ D1 ] = [ D414 ] и т.д. Соединив построенные точки отрезками, получаем развертку боковой поверхности наклонной призмы.
Чтобы получить полную развертку призмы, необходимо пристроить к ней НВ верхнего и нижнего оснований, как это показано в предыдущей задаче (рис.88).
 12.2.Развертка пирамиды
12.2.Развертка пирамиды
Построение развертки пирамиды сводится к многократному построению методом триангуляции натуральных величин треугольников, из которых состоит боковая поверхность пирамиды, плюс НВ основания. Для этого необходимо знать НВ всех ребер пирамиды.
Задача. Построить развертку усеченной пирамиды (рис.90).
Алгоритм решения
1. Определяем НВ ребер пирамиды.
Основание АВС параллельно П1 , поэтому ребра основания проецируются в П1 в натуральную величину.
Боковые ребра пирамиды – общего положения и для определения их НВ применяем метод вращения вокруг горизонтально проецирующей прямой i, проходящей через вершину пирамиды S. При вращении вокруг оси i точки А, В и С описывают окружности плоскости, которых перпендикулярны оси. В П1 эти окружности проецируются в НВ с центром в i1 , а на П2 – в виде отрезков, перпендикулярных i2. Поворачиваем горизонтальные проекции боковых ребер до параллельности оси проекций x12. Тогда в пространстве ребра расположатся параллельно П2 и спроецируются в эту плоскость в НВ. Находим проекции точек А, В и С в нужном нам положении (А2*, В2*, С2*) как результат пересечения линий связи, проведенных через А1*, В1*, С1* и траекторией перемещения фронтальных проекций точек А, В и С. Отрезки S2А2*, S2В2* и S2С2* натуральные величины боковых ребер.
Секущая плоскость S (S2) фронтально проецирующая и сечение проецируется на П2 в виде отрезка на вырожденной проекции плоскости, расположенного внутри очерка призмы. Вершины сечения на П2 находим как результат пересечения проекций ребер с S2 .
На натуральных величинах боковых ребер точки 12*, 22*, 32* находим по принадлежности соответствующим 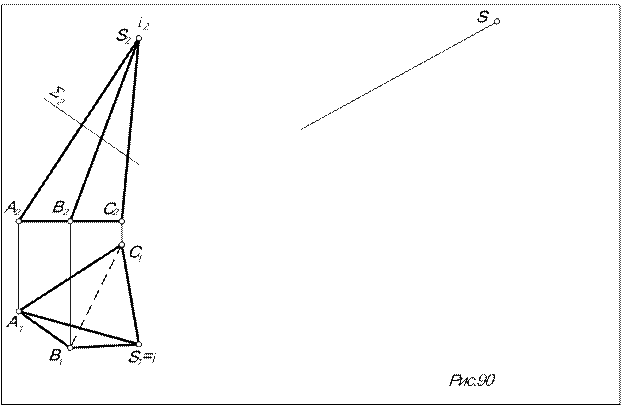 ребрам, проведя траектории точек при вращении ребер вокруг оси i.
ребрам, проведя траектории точек при вращении ребер вокруг оси i.
2. Строим развертку боковой поверхности.
На свободном поле чертежа проводим прямую и откладываем на ней НВ ребра SA = S2А2*. Методом триангуляции строим НВ грани SAB: из точки А, как из центра, проводим дугу радиусом, равным [ АВ ] = [ A1B1 ], а из точки S - дугу радиусом, равным [ SB ] = [ S2В2* ]. Точка пересечения этих дуг – вершина В на развертке. Соединив построенные точки, получаем НВ грани ASB. Наносим сторону (12) сечения, откладывая на стороне SA отрезок [ 1S ] = [ S212* ], а на стороне SB - отрезок [ 2S ] = [ S222* ]. По аналогичному алгоритму строим на развертке НВ граней BSC и ASC, нанося на них стороны сечения (23) и (31).
3. Строим полную развертку пирамиды, пристраивая к развертке боковой поверхности НВ основания и сечения, применяя метод триангуляции, как это показано на рис.88.
12.3.Развертка цилиндрической поверхности
Развертка боковой поверхности прямого кругового цилиндра радиуса R и высотой h представляет собой прямоугольник, одна из сторон которого равна длине 2pR окружности основания, а другая высоте h цилиндра.
Если цилиндр прямой усеченный или наклонный, строится приближенная развертка: в цилиндр вписывается n -угольная призма и строится ее развертка.
Задача. Построить развертку боковой поверхности прямого кругового цилиндра, усеченного плоскостью å (рис.91).
Алгоритм решения
1. Строим развертку боковой поверхности цилиндра в проекционной связи с его фронтальной проекцией (для удобства построений).
2. В цилиндр вписываем n -угольную (на рис.91 – 8ми-угольную) правильную призму и строим её развертку, которая и будет приближенной разверткой усеченного цилиндра. Окружность основания и длину развертки, равную 2pR, где R – радиус цилиндра, делим на 8 равных частей (от 0 до 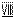 ). На П2 строим проекции ребер вписанной призмы (образующих цилиндра) и точек (12 … 82) пересечения их с секущей плоскостью å (å 2 ), как результат пересечения проекций образующих с вырожденной проекцией плоскости å 2.
). На П2 строим проекции ребер вписанной призмы (образующих цилиндра) и точек (12 … 82) пересечения их с секущей плоскостью å (å 2 ), как результат пересечения проекций образующих с вырожденной проекцией плоскости å 2.
 3. Через точки деления основания развертки проводим вертикальные отрезки, равные по величине образующим цилиндра, и находим на них точки 1…8,. проводя горизонтальные линии связи через проекции точек 12 … 82 до пересечения с соответствующей образующей.
3. Через точки деления основания развертки проводим вертикальные отрезки, равные по величине образующим цилиндра, и находим на них точки 1…8,. проводя горизонтальные линии связи через проекции точек 12 … 82 до пересечения с соответствующей образующей.
4. Построенные на развертке точки 1…8 соединяем плавной лекальной кривой. Это будет синусоида – развертка эллипса, сечения цилиндра плоскостью å. Фигура, ограниченная синусоидой, разверткой основания и образующими О и 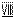 , является разверткой боковой поверхности усеченного цилиндра (окрашено серым цветом).
, является разверткой боковой поверхности усеченного цилиндра (окрашено серым цветом).
5. Чтобы построить полную развертку усеченного цилиндра, необходимо добавить еще НВ основания и сечения.
12.4.Развертка конической поверхности
Если задана поверхность прямого кругового конуса с радиусом основания R и высотой h, то развертка его боковой поверхности представляет собой круговой сектор, радиус которого равен длине образующей l конуса, а центральный угол j = 3600 ´ R/l.
Если конус усеченный, то строится его приближенная развертка – развертка усеченной n угольной пирамиды, вписанной в конус.
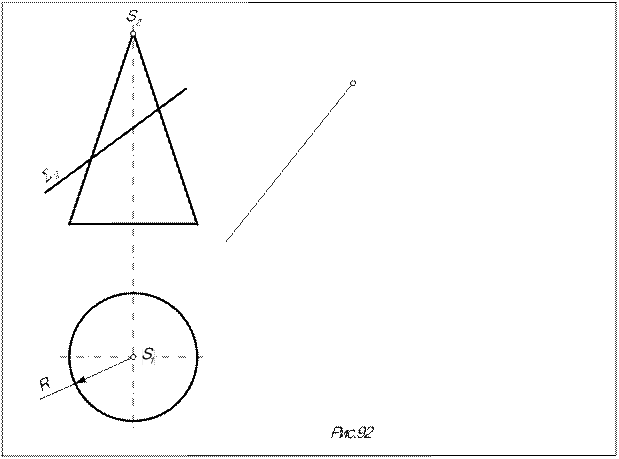
Задача. Построить развертку боковой поверхности конуса, усеченного плоскостью å (рис.92)
Алгоритм решения
1. Строим развертку прямого кругового конуса – круговой сектор с параметрами, указанными выше.
2. Вписываем в конус правильную n угольную (на рис.92 – 8 угольную) пирамиду, для чего делим окружность основания на 8 равных частей, находим точки деления 0 - 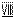 на П2 и соединяем полученные точки с проекцией вершины S2.
на П2 и соединяем полученные точки с проекцией вершины S2.
3. Находим фронтальные проекции 12 …82 точек пересечения ребер плоскостью å как результат пересечения вырожденной проекции плоскости å 2 с проекциями ребер и проводим через найденные точки проекции параллелей конуса – отрезки, перпендикулярные оси конуса.
4. Делим на 8 равных частей дугу – развертку основания конуса и точки деления соединяем с вершиной S на развертке.
5. Строим на развертке точки пересечения ребер вписанной пирамиды с плоскостью å как результат пересечения ребер с соответствующими проекциями параллелей на развертке. Параллели конуса развертываются в дуги, концентричные развертке основания, радиусы которых равны замеренному по очерковой образующей конуса расстоянию между фронтальной проекцией параллели и вершиной S2. Например, параллель, на которой расположены точки 2 и 6, разворачивается на развертке в дугу с центром в точке S и радиусом r2, 6.
6. Построенные на развертке точки 1…8 соединяем плавной лекальной кривой. Фигура, ограниченная этой кривой, разверткой основания и участками ребер 0 и 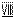 и будет разверткой боковой поверхности конуса, усеченного плоскостью å. Чтобы построить полную развертку усеченного конуса, необходимо добавить еще НВ основания и сечения.
и будет разверткой боковой поверхности конуса, усеченного плоскостью å. Чтобы построить полную развертку усеченного конуса, необходимо добавить еще НВ основания и сечения.
ЛИТЕРАТУРА
1. Начертательная геометрия. Конспект лекций для студентов машиностроительных специальностей.- Мариуполь, 1999.- 147 с.
2. Четверухин Н.Ф. Начертательная геометрия / В.С.Левицкий, З.И.Прянишникова, А.М.Тевлин, Г.И.Федотов.- М.: Высшая школа, 1963.- 420 с.
3. Фролов С.А. Начертательная геометрия / С.А.Фролов.- М.: Машиностроение, 1983. 240 с.
4. Рабочая тетрадь по начертательной геометрии.- Мариуполь, 2004.-46 с.
5. Методические указания по начертательной геометрии и черчению для студентов заочной формы обучения.- Мариуполь, 2004.- 49 с.