Лекция №3

Стерженнің созылуы мен сығ ылуы.

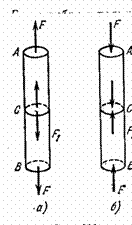
Біртекті стержен алып оның табандарына созушы жә не сығ ушы Ғ кү штерін тү сірейік. Стержен деформацияланады, яғ ни созылады немесе сығ ылады. Ойша белгілі бір стержен осьіне перпендикуляр С осін жү ргізейік. АС стерженнің тепе- тең дігі ү шін оның тө менгі С табанына Ғ =F кү ші ә сер етуі керек. Бұ л кү ш стерженінің жоғ ары стержанді тарту немесе оны сығ у кү шіне тең. Бұ л кү штің пайда болу себебі оның тө менгі бө лігінің деформацияланғ андығ ы. Стерженнің жоғ арғ ы бө лігі де деформацияланғ ан жә не тө менгісіне осындай, бірақ қ арама- қ арсы бағ ытталғ ын кү ші ә сер етеді. Мұ ндай кү штер созылғ ан немесе сығ ылғ ан стерженнің кез келген кө лденең қ имасына ә сер етеді. Осылайша, стерженнің деформациялануы серпімді кү штердің пайда болуына жә не стерженнің ә рбір шекаралас бө лігі бір – біріне сол кү шпен ә сер етуіне байланысты. Стерженнің кө лденең қ имасының бірлік ауданына тура келетін кү ш шамасын кернеу деп атаймыз. Қ арастырылып отырғ ан жағ дайдакернеу стерженнің кө лденең қ имасына перпендикуляр. Егер стержен созылғ ан болса, онда кернеу созылғ ан кернеу деп аталады жә не мына ө рнекпен анық талады:

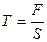
Мұ ндағ ы S-Стерженнің кө лденең қ имасының ауданы. Егер стержен сығ ылғ ан болса, онда кернеу қ ысым деп аталады жә не мына ө рнек арқ ылы анық талады: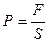

Қ ысымды теріс таң бамен алынғ ан созылу кернеуі деп қ арастыруғ а болады жә не керә сінше яғ ни

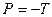
Бұ л бізге созылу мен сығ ылуды жеке-жеке қ арастыру қ ажеттілігін туғ ызбайды.

2. 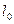-деформацияланбағ ан стерженнің ұ зындығ ы болсын. F кү ші тү сірілген соң оның ұ зындығ ы ө згеріске ұ шырайды жә не 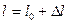тең болады

қ атынасы салыстырмалы ұ зару деп аталады. Созушы кү штер ә сер еткенде ол оң болады, ал сығ ушы кү тер ә сер етсе, ол теріс болады. Теріс таң бамен алынғ ан салытырмалы ұ зару салыстырмалы сығ ылу деп аталады. Осылайша анық тама бойынша салытырмалы сығ ылу - 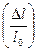тең. Ол оң болады егер сығ ылу кү штер ә сер етсе, теріс, созушы кү штер ә сер етсе.

Тә жірибе кө рсеткендей ү лкен емес серпімді деформациялар ү шін созушы кернеу салыстырмалы ұ заруғ а пропорционал:

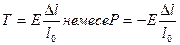
Мұ ндағ ы Е стерженнің материалына жә не физикалық кү йіне тә уелді тұ рақ ты. Ол Юнг модулі (1773-1829) деп аталады. 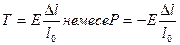тең деу стерженнің созылу жә не сығ ылу деформациялары ү шін Гук заң ын кө рсетеді. Бұ л шамалап келтірілген заң. Ол ү лкен деформациялар ү шін орындалмауы мү мкін. Гук заң ы орындалатын деформациялар кіші деформациялар деп аталады. Егер 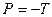тең деуіне қ ойсақ, онда болады. Сондық тан Юнг модулін кө біне стержен екі есе ұ заратындай етіп кү ш тү сіру арқ ылы анық тайды. Бірақ бұ л жағ дайда Гук заң ы орындалмай қ алады. Бұ л заң ның кемшілігі барлық ү лкен деформациялар ү шін Гук заң ы орындалмай қ алуында: дене не сынады, не деформация мен тү сірілген кү штің арасындағ ы пропорционалдық бұ зылады.

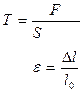
Т-кернеу, Е-Юнг модулі, 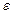-салыстырмалы ұ зару, Р-қ ысым кү ші

Р=-Т

Р=-Е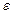

Т=-Е 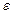-Гук заң ы

стержннің созылуы

Юнг модулі ә р тү рлі заттар ү шін шамасы ә р тү рлі болады.Кейбір жағ дайларда Юнг модулін анық тау ү шін стержнді бастапқ ы ұ заруынан 2 есе ұ зарту керек.

3.Гук заң ына қ арағ анда кө бірек жалпыланғ ан заң бқ ұ л кепілді деформация кезінде созушы кернеу Т салыстырмалы ұ зарудың функция болады деген заң, яғ ни Т=T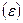

Бұ л функция нольге тең есуі тиіс, егер 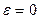болса, себебі деформация жоқ кезде, созушы кернеу де жоқ болады.

Т=Е бұ л формула дұ рыс емес. Бұ л жағ дайда Гук заң ы орындалмайды.

Кейбір жағ дайларда салыстырмалы ұ зындық ты анық тау ү шін

жә не формулаларынан қ айсысы тиімді екенін білу ү шін екеуінің айырымын табу керек.

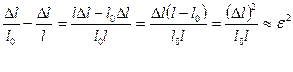
Егер

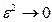
Сонда екі формуланы да пайдалануғ а болады. Жалпы алғ анда механикалық кернеу салыстырмалы деформацияның функциясы болады. Ол функцияның тү рі іспеттес

Егер бірінен соң бір кернеу стержнге ә сер ететін болса,

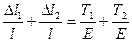
яғ ни бұ л жағ дайда суперпозиция принципін пайдалануғ а болады.

Бұ л келтірілген анық тама тек созылу мен сығ ылу деформациясына ғ ана емес, сонымен қ атар барлық кіші деформациялар ү шін орындалады.Егер деформациялар кіші болса, онда денелердің серпімді тұ рақ тылары ө згермейді.Бұ л жерден егер денеге бірнеше кү ш ә сер етсе, онда қ орытқ ы деформацияны есептеу ү шін орындалады. Егер деформациялар кіші болса, онда қ орытқ ы деформацияны еесптемеу ү шін алдымен ә рбір кү штің ә серінен пайда болғ ан денформацияларды (басқ а кү штер болмады деп есептеп) есептеп алып, оларды қ оссақ болғ аны. Бұ л кіші деформацияларды суперпозиция принфципі деп атайды.

5. Денені деформациялау ү шін денеге қ атысты жұ мыс жасау керек. Сонымен ірге деформацияланғ ан дененің ө зі жұ мыс жасацйды. Оның потенциалдық энергиясы артық болады. Бұ л энергия серпімді энергия деп аталады. Бұ л энергия денені деформациялағ анда жасағ ан жұ мысқ а тең, сонымен бірге бұ л жұ мыс толығ ымен дененің кинетикалық эгерг.иясын арттыруғ а емес, тек серпімді энергияны арттыруғ а тиіс.Кинетикалық энергияның пайда болмауы ү шін деформацияны ө те баяу жү ргізуі тиіс. Сыртқ ы кү штерде дене ә рқ ашан тепе-тең дік жағ дайында болатындай етіп біркелкі ө сіру керек.Басқ а сө збен айтқ анда, деформация кезінде сыртқ ы кү штер ә рқ ашан пайда болып отыратын ішкі кернеу кү штерімен тең есіп отыру керек. Егер осы шарт орындалса, онда квазистатикалық процес жү ріп жатыр деп есептеуге болады.

Мұ ны кө рсету ү шін деформацияланғ ан дененің моделі бола алатын спиральді серіппені алайық. Оны жоғ ары жағ ынан бекітіп қ оялық. Тө менгі жағ ына жіп ілге, нде серіппе созылып кетпес ү шін қ олымызбен ұ стап тұ рамыз. Егер жү кті бірден жіберсек тербелістер пайда болады.Жү к салмағ ының жасағ ан жұ мысы тек серіппені созуғ а ғ ана емес, серіппе жә не жү ктің кинетикаклық энергиясын арттыруғ а да жұ мсалады.Бұ л квазистатикалық процесс емес.Серіппенің серпімді энергиясын есептеу ү шін мұ ндай процес жарамайды. Енді серіппенің тө менгі жағ ына ө те жең іл чашка ілейік жә не оны ө те баяу толығ ырақ толтырып отырайық. Тербеліс пайда болмайды, серіппе баяу жә не ү здіксіз салмақ артқ ан сайын созылады. Ауыцрлық кү шінің жалпы жұ мысы деформациаланғ ан серіппенің потенциалдық энергиясын артыруғ а жұ мсалады. Бұ л процесс квазистатикалық жә не оны серіппенің серпімді энергиясын есептеуге қ олдануғ а болады.

6. Бұ л ескертулерден кейін созылғ ан стерженнің серпімді энергиясын есептеу қ иын емес. Стерженге созушы f кү шін тү сірейік жә не оны бастапқ ы f=0 мә нінен соң ғ ы f=F мә ніне дейін жоғ арылатайық. Бұ л кезде стерженнің созылуы Х=0 мә нінен 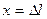мә ніне дейін ө згереді.

Гуке заң ы бойынша , мұ ндағ ы К- Юнг модулі арқ ылы оң ай ө рнектеуге болатын қ атаң дық коэффициенті. Қ арастырылып отырғ ан процессте барлық жұ мыс энергияны серпімді арттыруғ а жұ мсалады. Сондық тан

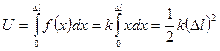
Егер соң ында 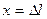болса, онда 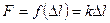Осыны ескере отырып, мынаны алмыз

Егер деформацияланғ ан стерженге бірден тұ рақ ты Ғ кү шін тү сіргенде, онда 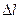ұ заруғ а екі есе кө п А=f 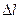жұ мысы жасалғ ан болар еді. Серпімді потенциялды энергияның қ алдығ ы тура сол болғ андық тан А жұ мысының жартысы ғ ана серпімді энергияны арттыруғ а жұ мсалатыны тү сінікті. Бұ л жұ мыстың екінші жартысы стерженге квазистатикалық емес ә сер ету кезінде пайда болатын тербелістермен толқ ындардың кинетикалық энергиясын арттыруғ а жұ мсалады. Міне сондық тан

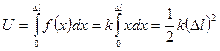
тең діктерінің алдына ½ коэффициенті пайда болды.

Серпімді энергияның кө лемдік тығ ыздығ ын табайық, яғ ни созылғ ан (немесе сығ ылғ ан) стерженнің бірлік кө леміне сә йкес келетін энергияны есептейік. Ол

тең дігін V=Sl кө лемге бө лу арқ ылы табылады. Онда мынаны аламыз:

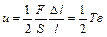
Егер Гук заң ын қ олдансақ, онда бұ л формуланы мына тү рде жазу қ иын емес:

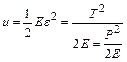
Серпімділік энергиясын анық тау ү шін ә сер етуші кү шті интегралдау керек.

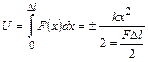
Кө лемге келетін бірлік энергияны оның тығ ыздығ ы деп атаймыз.Ол мына формула бойынша есептелінеді.

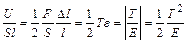
7. Тә жірибе кө рсеткендей, созушы немесе сығ ушы Ғ кү шінің ә серінен стержень тек ұ зынынан ғ ана емес, кө лденең іненде ө згереді. Егер Ғ - созушы кү ш болса, онда кө лденең ө лшемдер кішірейеді. Егер сығ ушы кү ш ә сер етсе, онда ү лкейеді. Егер - стержньнің деформацияғ а дейінгі қ алың дығ ы,

-деформациядан кейінгі стержень қ алың дығ ы. Дө ң гелек стержень ү шін қ алың дық деп оның диаметрін, тікбұ рышты стержень ү шін –оның тікбұ рышты табанының бір қ абырғ асын алуғ а болады жә не т.с.с.

Серпінділік қ асиетін кө рсететін тұ рақ ты шамалардың бірі Пуассон коэффициенті.

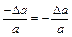
стерженнің салыстырмалы кө лденең сығ ылуы деп аталады.

--кішірейген кө лденең қ има.

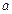-бастапқ ы кө лденең қ има

Салыстырмалы кө лденең сығ ылудың сә йкес салыстырмалы ұ заруғ а қ атынасы Пуассон коэффициенті деп аталады. Бұ л атау француз ғ алымы Симеон Пуассон (1781-1840) есімімен алынғ ан.

Пуассон коэффициенті дененің тек материалына тә уелді жә не оның серпімділік қ асиеттерін сипаттайтын ең негізгі тұ рақ тылардың бірі. Сығ ушы кү штерді ерекше қ арастырмаймыз, себебі сығ ушы кү шті қ арама –қ арсы таң бамен алынғ ан созушы кү ш деп алуғ а болады.

Юнг модулі Е жә не 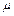Пуассон коэффициенті изотропты материалдың серпімді қ асиеттерін толығ ымен сипаттайды. Басқ а серпімді тұ рақ тыларды Е жә не 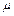арқ ылы ө рнектеуге болады.

8. Соң ында, басқ а барлық біз қ арастырғ ан жә не қ арастыратын серпімділік модульдері мен коэффициенттері негізінде изотермиялық модульдер жә не коэффициенттер деп аталуы тиіс.Олар температурасы тұ рақ ты жағ дайдағ ы деформацияны сипаттайды.Бұ л статикалық деформация кезінде орындалады. Бірақ егер деформациялар динамикалық (мысалы, серпімді ортадағ ы толқ ындар) болса, онда олардың тез болғ андығ ы соншалық деформация кезінде пайда болғ ан температуралар айырмасы жылу алмасу нә тижесінде тең есіп ү лгермейді. Егер ортаның ә ртү рлі қ ызғ ан бө ліктері арасында жылу алмасу болмағ анда ерекше жағ дай орын алады. Бұ л процесске сә йкес келетін серпімділік модульдері мен коэффициенттері адиабаталық деп аталады.