
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Иілу деформациясы.
|
|
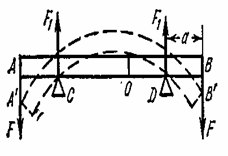
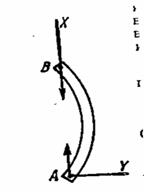
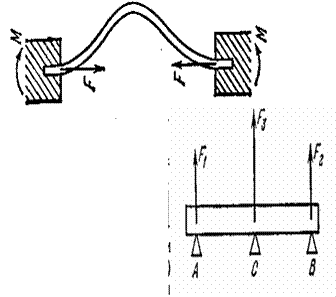
Белгілі кө лденң қ имсаы біртекті балканың иілуін қ арастырайық. Сонымен қ атар балканың кө лденең қ имасы, ұ зындығ ы бойымен бірдей болуы тиіс. Балканың формасы деформацияғ а дейін тік сызық ты болсын. Балка осіне жанама АВ жә не А'В' қ има жү ргізейік, ойша одан АА'ВВ' шексіз кіші элемент бө ліп алайық жә не оның ұ зындығ ын 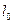 деп белгілейік. Бө ліп алынғ ан элементтің шексіз кішілігін ескеріп иілу нә тижесінде АА'ММ'ВВ' жә не оларғ а парлель борлық басқ а тузулер центірі о осінде жатқ ан шең берлерге айналады. Бұ л ось иілу осьі деп аталады.ММ' сызығ ынан сыртқ ы жатқ ан сызық тар иілгенде ұ зарады, ал ММ' сызығ ының ішкі бө лігінде жатқ ан сызық тар кішірейтіледі. Сонымен ММ' сызығ ының ұ зындығ ы ө згеріссіз қ алады. Бұ л сызық нейтраль сызық деп аталады.
деп белгілейік. Бө ліп алынғ ан элементтің шексіз кішілігін ескеріп иілу нә тижесінде АА'ММ'ВВ' жә не оларғ а парлель борлық басқ а тузулер центірі о осінде жатқ ан шең берлерге айналады. Бұ л ось иілу осьі деп аталады.ММ' сызығ ынан сыртқ ы жатқ ан сызық тар иілгенде ұ зарады, ал ММ' сызығ ының ішкі бө лігінде жатқ ан сызық тар кішірейтіледі. Сонымен ММ' сызығ ының ұ зындығ ы ө згеріссіз қ алады. Бұ л сызық нейтраль сызық деп аталады.
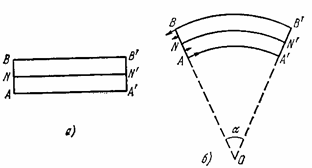 |
1а –суреттің жазық тығ ына перпендикуляр нейтраль сызық арқ ылы ө тетін деформацияланғ ан балка қ имасы нейтраль қ има деп аталады. Осылайша сыртқ ы сызық тар созылғ ан, ал ішкі сызық тар сығ ылғ ан болады. ММ' нейтраль сызық тың радиусы 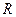 болсын. (Нейтраль қ имадан
болсын. (Нейтраль қ имадан  қ ашық тық та жатқ ан) онда
қ ашық тық та жатқ ан) онда  болады. Мұ ндағ ы
болады. Мұ ндағ ы 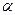 ММ' доғ аның орталық бұ рышы. Нейтраль қ имадан
ММ' доғ аның орталық бұ рышы. Нейтраль қ имадан 
қ ашық тық та жатқ ан сызық ты қ арастырайық.  оң, егер сызық нейтроль қ имадан жоғ ары жатса, ал тә мен жатса теріс. Егер балка онша қ алың болмаса, яғ ни
оң, егер сызық нейтроль қ имадан жоғ ары жатса, ал тә мен жатса теріс. Егер балка онша қ алың болмаса, яғ ни  , онда қ арстырылып отырғ ан сызық қ а ә сер етуші тартылыс мынағ ан тең:
, онда қ арстырылып отырғ ан сызық қ а ә сер етуші тартылыс мынағ ан тең:
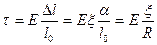
Осылайша тартылыс қ ашық тық қ а байланысты сызық ты ө згереді. Ол нейтраль сызық тың тә рбиеө менгі жағ ында теріс болады, яғ ни кернеу болып табылады. Тартылыс кү штері мен кернеудің қ осындысы нө лден ө згеше болуы мү мкін. Брақ бұ л жағ дайда балканың иілуіне барлық сызық тары ү шін бірдей тартылыс жә не сығ ыу кү штері ә сер етеді. Мұ ны ерекше ескеріп, иілуді қ арастырғ анда ескермеуге болады. С тан барлық тартылыс кү штерінің қ осындысы нө лге тең деп қ арастырымыз.
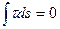 немесе
немесе 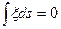
Мұ ндағ ы  -қ арастырылып отырғ ан кө лденең қ иманың аудан элементі Интегралдау кө лденең қ иманың барлық бө лігі бойынша жү ргізіледі. Осыдан біз нейтраль сызық жә не нейтраль қ има кө лденең қ иманың ауырлық центірінен ө тетінін байқ аймыз.
-қ арастырылып отырғ ан кө лденең қ иманың аудан элементі Интегралдау кө лденең қ иманың барлық бө лігі бойынша жү ргізіледі. Осыдан біз нейтраль сызық жә не нейтраль қ има кө лденең қ иманың ауырлық центірінен ө тетінін байқ аймыз.
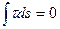 болғ андық тан созушы кү штер АВ қ имасына ә сер етпейтін болады. Осы жазық тық қ а перпендикуляр осьті алайық.
болғ андық тан созушы кү штер АВ қ имасына ә сер етпейтін болады. Осы жазық тық қ а перпендикуляр осьті алайық.
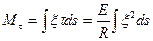 немесе
немесе 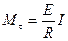 мұ нда
мұ нда 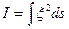
 -шамасы инертция моменті деп аталады.
-шамасы инертция моменті деп аталады.
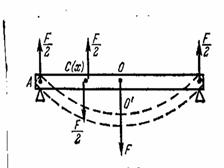
Егер балка екі а жә не в тіктө тбұ рышты формалы болса, онда:
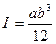
Дә ң гелек радиусы 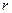 кө лденең қ иманың инертция моменті:
кө лденең қ иманың инертция моменті:
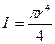
Ішкі диаметрі 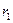 жә не сыртқ ы
жә не сыртқ ы 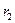 цилиндрлік труба ү шін:
цилиндрлік труба ү шін:
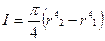
 | |||
 |
 |  | ||
Кез келген ортада таралатын тербелісті толқ ындар деп атайды. Ол толқ ындар ө рістерде де таралуы мү мкін.
Серпімді толқ ындар деп серпімді орталарда тарайтын механикалық тербелістерді айтамыз. (деформацияларды айтуғ а болады)
Толқ ын туғ ызатын сыртқ ы денелерді толқ ын кө здері деп атайды.
Толқ ындар қ ума жә не кө лденең болып бө лінеді.
Қ ума толқ ындар қ атты, сұ йық, газдарда да тарала береді, ал кө лденең толқ ындар тек қ ана қ атты денеде таралады.
Толқ ынның таралу бағ ыты мен ортаның бө лшектерінің қ озғ алу бағ ыты сә йкес болса, мұ ндай толқ ындарды қ ума толқ ындар деп атайды.
Егер толқ ынның таралу бағ ыты мен ортаның бө лшектерінің қ озғ алу бағ ыты перпендикуляр болса, мұ ндай толқ ындарды кө лденең толқ ындар деп атайды.
Бұ л толқ ындардан бө лек беттік толқ ындар деген сұ йық тарда кездесетін толқ ын тү рі де бар.


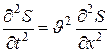
Сфералық толқ ын болса, онда:
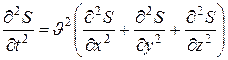
Жалпы толқ ындық тең деуді анық тау ү шін.
Кез келген векторлық ө ріс шексіздікте 0-ге тең болу ү шін мынандай шарт болу керек.
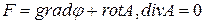
j-скалярлық потенциал
А-векторлық потенциал
Осы шартты пайдалана отырып, серпімді қ ума толқ ынның тең деуін жазуғ а болады.

D-Лаплас операторы.
 - Даламбер операторы.
- Даламбер операторы.
Кө лденең толқ ынның тең деуі:
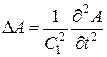
Беттік толқ ынның жылдамдығ ы:

Толқ ын таралғ ан кезде ортаның тығ ыздығ ы жә не қ ысым ө згереді. Сол ө згеріс тең дігін былай жазуғ а болады.
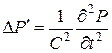

Синусоидалық толқ ындар ү шін Гелм-Голцтің тең деуі былай болады.