
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Современная теория портфеля Г. Марковица
|
|
Новый подход к диверсификации портфеля был предложен Гарри Марковичем, основателем современной теории портфеля (1952 г.).
По мнению Марковица, инвестор должен принимать решение по выбору портфеля исходя исключительно из показателей ожидаемой доходности и стандартного отклонения доходности. Это означает, что инвестор выбирает лучший портфель, основываясь на соотношении этих двух параметров. При этом интуиция играет определяющую роль.
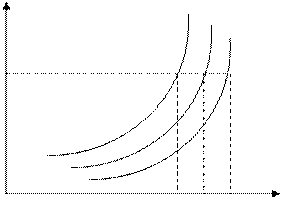
Метод, применяемый при выборе оптимального портфеля, использует так называемые кривые безразличия. Они отражают отношение инвестора к риску и доходности.
 Доходность,
Доходность, 
А В С
D
Риск, s
Рис. 5. Кривые безразличия инвестора
Таким образом, кривые могут быть представлены как график, на котором по горизонтальной оси откладываются значения риска, мерой которого является стандартное отклонение, а по вертикальной оси – величины вознаграждения, мерой которого служит ожидаемая доходность. Первое важное свойство кривых безразличия состоит в том, что все портфели, представленные на одной заданной кривой безразличия, равноценны для инвестора.
Кроме того, график позволяет сделать вывод о том, что для инвестора всегда будет более привлекательным портфель, расположенный на кривой, которая находится выше и левее (т. В), чем портфель, расположенный на кривой, лежащей ниже и правее (т. D), так как при том же уровне риска, он обеспечивает более высокий уровень дохода. Также для инвестора более привлекательным будет тот портфель, который при том же уровне дохода дает меньший риск (т.А и т.С).
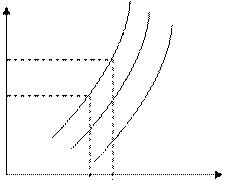 Исходя из отношения инвестора к риску и доходности и их оценок инвестор может иметь бесконечное число кривых безразличия. Степень крутизны кривых свидетельствует об индивидуальном для каждого инвестора соотношения риска и доходности.
Исходя из отношения инвестора к риску и доходности и их оценок инвестор может иметь бесконечное число кривых безразличия. Степень крутизны кривых свидетельствует об индивидуальном для каждого инвестора соотношения риска и доходности.
 |
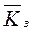
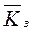
s s
а) крутые кривые б) пологие кривые
Рис. 6. Виды кривых безразличия
В первом случае (а) инвестор готов допустить малое увеличение риска лишь с компенсацией в виде значительного увеличения доходности. Во втором случае (б) инвестор ради небольшого увеличения доходности готов принять значительное увеличение риска.
Итак, главными параметрами при управлении портфелем, которые необходимо определить менеджеру, являются ожидаемая доходность и риск. Формируя портфель, менеджер не может точно определить будущую динамику его доходности и риска, поэтому свой выбор он строит на ожидаемых значениях.
Поскольку портфель, формируемый инвестором, состоит из набора различных ценных бумаг, его доходность и риск будут зависеть от доходности и риска каждой отдельной ценной бумаги. Кроме того, ожидаемая доходность портфеля зависит от размера начального капитала, инвестированного в конкретные ценные бумаги.
Ожидаемая доходность портфеля может быть вычислена двумя способами. Первый способ основан на использовании стоимостей на конец периода и заключается в вычислении ожидаемой цены портфеля в конце периода и уровня его доходности:
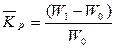 (1)
(1)
где: 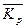 – ожидаемая доходность портфеля;
– ожидаемая доходность портфеля;
W0 – начальная стоимость портфеля;
W1 – ожидаемая стоимость портфеля в конце периода.
Второй способ построен на использовании ожидаемой доходности ценных бумаг и включает вычисление ожидаемой доходности портфеля как средневзвешенной ожидаемых доходностей ценных бумаг, входящих в портфель. Относительные рыночные курсы ценных бумаг портфеля используются в качестве весов:
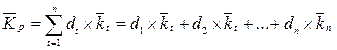 (2)
(2)
где: dt – доля начальной стоимости портфеля, инвестированная в ценную бумагу;
kt – ожидаемая доходность ценной бумаги;
n – количество ценных бумаг в портфеле.
Инвестиционный риск портфеля определяется как изменчивость доходности, которая измеряется стандартным отклонением (дисперсией) распределения доходности портфеля.
Ожидаемый риск портфеля представляет собой сочетание стандартных отклонений (дисперсий) входящих в него ценных бумаг. Однако в отличие от ожидаемой доходности риск портфеля не является обязательно средневзвешенной величиной стандартных отклонений доходности ценных бумаг. Дело в том, что различные ценные бумаги могут по-разному реагировать на изменение конъюнктуры рынка. В результате стандартные отклонения доходности различных ценных бумаг в ряде случаев будут гасить друг друга, что приведет к снижению риска портфеля. Риск портфеля зависит от того, в каком направлении и в какой степени меняются доходности входящих в него ценных бумаг при изменении конъюнктуры рынка.
Для определения взаимосвязи и направления изменения доходностей ценных бумаг используют показатель ковариации и коэффициент корреляции.
Показатель ковариации определяется по формуле
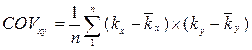 (3)
(3)
где: COV – ковариация доходности ценных бумаг;
kx, y – норма дохода по ценной бумаге;
 – ожидаемая норма дохода по ценной бумаге;
– ожидаемая норма дохода по ценной бумаге;
n – число наблюдений за доходностью ценных бумаг.
Положительное значение ковариации свидетельствует, что доходность ценных бумаг изменяется в одном направлении, отрицательное – что в обратном. Нулевое значение ковариации означает, что взаимосвязь между доходностями активов отсутствует.
Другим показателем взаимосвязи изменения доходностей ценных бумаг служит коэффициент корреляции (rxy):
 (4)
(4)
где: sх, sу — стандартное отклонение доходности ценной бумаги х и у
Коэффициент корреляции меняется в пределах от –1 до +1. Положительное значение коэффициента говорит о том, что доходности ценных бумаг меняются в одном направлении с изменением конъюнктуры, отрицательное – что в противоположном. При нулевом значении коэффициента корреляции связь между доходностями ценных бумаг отсутствует.
Эффективная диверсификация по Марковицу предусматривает, что чем ниже коэффициент корреляции ценных бумаг, входящих в портфель, тем менее рискованным будет портфель.
Исходя из формулы расчета корреляции можно вывести новую формулу для определения ковариации:
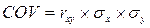 (5)
(5)
Для расчета стандартного отклонения (s) ценной бумаги используется формула:
 (6)
(6)
где: ki – конкретное значение возможных вариантов дохода;
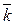 – ожидаемое среднее значение дохода;
– ожидаемое среднее значение дохода;
Pi – вероятность получения i -го варианта дохода;
N – число вероятностей.
Стандартное отклонение характеризует степень колеблемости изучаемого показателя. В отношении ценных бумаг этот показатель, как правило, показывает максимальное отклонение дохода от нормы в сторону увеличения и уменьшения. Таким образом, при расчете данного показателя инвестор сможет увидеть, какой максимальный размер снижения дохода он может понести.
Пример. Рассчитать ковариацию портфеля, состоящего из двух ценных бумаг, если коэффициент корреляции равен 0, 7, и прогнозируются следующие вероятности получения дохода по ним:
| Показатель | Ценная бумага А | Ценная бумага Б | ||
| 1 | 2 | 1 | 2 | |
| Доход, тыс. руб., Кi | 100 | 120 | 90 | 110 |
| Вероятность получения дохода, Рi | 0, 4 | 0, 6 | 0, 3 | 0, 7 |
Рассчитаем среднюю ожидаемую доходность 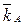 и
и 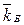
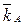 = 100 ´ 0, 4 + 120 ´ 0, 6 = 112 тыс. руб.
= 100 ´ 0, 4 + 120 ´ 0, 6 = 112 тыс. руб.
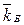 = 90 ´ 0, 3 + 110 ´ 0, 7 = 104 тыс. руб.
= 90 ´ 0, 3 + 110 ´ 0, 7 = 104 тыс. руб.
Тогда sА и sБ будут равны:
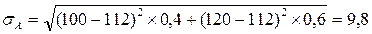

Значит отклонение доходности по ценной бумаге «А» составляет 9, 8 тыс. руб., а значит она является более рискованной, чем ценная бумага «Б».
Тогда ковариация между ценными бумагами «А» и «Б» составит:
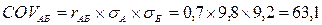
Положительное значение ковариации свидетельствует о том, что доходности ценных бумаг «А» и «Б» изменяются в одном направлении.
Мы рассмотрели отклонение (уровень риска) для отдельной ценной бумаги. Уровень риска портфеля, состоящего из двух ценных бумаг, рассчитывается по формуле:
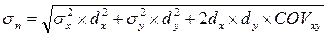 (7)
(7)
где: s — стандартное отклонение по портфелю;
sx, y – стандартное отклонение по ценной бумаге;
dx, y – доля ценной бумаги в портфеле.
Для оценки риска портфеля, объединяющего большее число ценных бумаг, требуется проведение большого объема вычислений, поэтому они выполняются, как правило, с помощью использования специальных статистических компьютерных программ.
Модель ценообразования на капитальные активы (capital assets pricing model, CАРМ)
Данная модель основывается на том факте, что инвесторы, вкладывающие свои средства в рисковые активы, ожидают некоторого дополнительного дохода, превышающего безрисковую ставку дохода, как компенсацию за риск владения этими активами. Подобное требование описывается техническим термином «неприятие риска». He принимающие риск инвесторы не обязательно избегают его. Однако они требуют компенсацию в форме дополнительного ожидаемого дохода за принятие риска по инвестициям, доходность по которым не является гарантированной.
Другими словами, САРМ предполагает, что норма дохода по рисковому активу складывается из нормы дохода по безрисковому активу (безрисковой ставки) и премии за риск, которая связана с уровнем риска по данному активу:
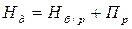 (8)
(8)
Для измерения величины систематического риска существует специальный показатель – коэффициент b. Он характеризует неустойчивость (изменчивость) дохода отдельной ценной бумаги или другого финансового инструмента относительно доходности рыночного портфеля. В западных странах данные по b-коэффициенту публикуются в открытой печати, но его можно рассчитать, используя следующую формулу:
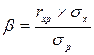 (9)
(9)
где: rxp – корреляция между доходностью ценной бумаги х и средним уровнем доходности ценных бумаг на рынке;
sх – стандартное отклонение доходности по конкретной ценной бумаге;
sр – стандартное отклонение доходности по рынку ценных бумаг в целом.
Уровень риска отдельных ценных бумаг определяется на основе таких значений:
b = 1 – средний уровень риска;
b > 1 – высокий уровень риска;
b < 1 – низкий уровень риска.
Для расчета b по портфелю рассчитывается как средневзвешенный b-коэффициент отдельных видов входящих в портфель инвестиций, где в качестве веса берется их удельный вес в портфеле:
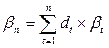 (10)
(10)
где: dt – удельный вес t-го актива в портфеле;
bt – коэффициент b для t-го актива;
n – число активов в портфеле.
Таким образом, формула расчета доходности портфеля или актива (ценной бумаги) принимает следующий вид:
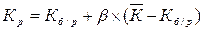 (11)
(11)
где: Кр – требуемая норма прибыли ценной бумаги (портфеля);
Кб/р – безрисковая рыночная ставка;
b – коэффициент данной ценной бумаги (портфеля);
К – ожидаемая норма прибыли ценной бумаги.
Таким образом, чем более рисковой является ценная бумага, т.е. чем больше b, тем больше должен быть и доход, который она приносит, и наоборот.