
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задание 2.3.1. Схема Бернулли
|
|
1. Для данного участника игры вероятность набросить кольцо на колышек равна 0, 3. Какова вероятность того, что при 6 бросках 3 кольца окажутся на колышке, если считать броски независимыми?
2. У игрока 5 шариков, которые он бросает до первого попадания или до полного израсходывания всех шариков. Найдите вероятность того, что не все шарики будут израсходованы, если вероятность попадания при одном броске равна 0, 1.
3. Вероятность наличия опечатки на странице книги равна 0, 0025. Какова вероятность того, что из 400 страниц опечатки имеются только на пяти страницах?
4. Какова вероятность того, что при десяти бросаниях игрального кубика тройка выпадет от двух до четырех раз?
5. На самолете имеются 4 одинаковых двигателя. Вероятность нормальной работы каждого двигателя в полете равна р. Найдите вероятность того, что в полете могут возникнуть неполадки в одном двигателе.
6. Из полного шахматного набора 9 раз извлекается фигура, которая затем возвращается. Какова вероятность того, что при этом конь появится ровно три раза?
7. Вероятность отказа каждого прибора при испытании равна 0, 4. Что вероятнее ожидать: отказ двух приборов при испытании четырех или отказ трех приборов при испытании шести, если приборы испытываются независимо друг от друга?
8. Вероятность того, что на некотором предприятии расход электроэнергии не превысит суточной нормы, равна 0, 8. Какова вероятность того, что в течение пяти рабочих дней из семи перерасхода электроэнергии не будет?
9. Стрелок попадает в цель с вероятностью 0, 8. Какова вероятность поражения цели при пяти выстрелах?
10. В горном районе создано n автоматических сейсмических станций. Каждая станция в течение года может выйти из строя с вероятностью р. Какова вероятность того, что в течение года хотя бы одна станция потребует ремонта?
11. Вероятность появления события А хотя бы один раз при пяти независимых испытаниях равна 0, 99757. Какова постоянная вероятность появления этого события при одном испытании?
12. Известно, что 5% радиоламп, изготовляемых заводом, являются нестандартными. Из большой партии (независимо друг от друга) производится случайная выборка радиоламп. Сколько ламп нужно взять, чтобы с вероятностью не менее 0, 9 была извлечена хотя бы одна нестандартная лампа?
13. Вероятность попадания в цель при каждом выстреле равна 0, 2. сколько нужно произвести независимых выстрелов, чтобы с вероятностью не менее 0, 99 в мишени была бы хотя бы одна пробоина?
14. При высаживании непикированной рассады помидоров только 80% растений приживаются. Найдите вероятность того, что из 10 посаженных кустов помидоров приживется не менее 9.
15. Контрольная работа состоит из 4 вопросов. На каждый вопрос приведено 5 ответов, один из которых правильный. Какова вероятность того, что при простом угадывании правильный ответ будет дан не менее чем на 3 вопроса?
Задание 2.3.2.Приближенные формулы Лапласа и Пуассона
1. Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0, 8. Найти вероятность того, что в 1600 испытаниях событие наступит 1200 раз.
2. Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0, 02. Найти вероятность того, что в 150 испытаниях событие наступит 5 раз.
3. В партии из 1000 изделий имеются 10 дефектных. Найти вероятность того, что среди 50 изделий, взятых наудачу из этой партии, ровно три окажутся дефектными.
4. Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0, 8. Найти вероятность того, что в 125 испытаниях событие наступит не менее 75 и не более 90 раз.
5. В результате проверки качества приготовленного для посева зерна было установлено, что 80% зерен всхожие. Определить вероятность того, что среди отобранных и высаженных 100 зерен прорастет не менее 70.
6. Вероятность того, что пара обуви, взятая наудачу из изготовленной партии, окажется первого сорта, равна 0, 7. определить вероятность того, что среди 2100 пар, поступающих на контроль число пар первосортной обуви окажется не менее 1000 и не более 1500?
7. Вероятность рождения мальчиков р = 0, 515. Какова вероятность, что из 1000 рождающихся детей мальчиков будет 520?
8. В ОТК с конвейера для проверки поступила партия изделий в количестве 600 штук. Какова вероятность того, что среди этих изделий имеется 500 изделий 1-го сорта, если известно, что с конвейера в среднем поступает 85% продукции 1-го сорта?
9. Книга в 500 страниц содержит 50 опечаток. Оценить вероятность того, что на случайно выбранной странице не менее 3 опечаток.
10. Вероятность изготовления бракованного изделия равна 0, 001. вычислить вероятность того, что контролер, проверяющий партию в 200 изделий, обнаружит число бракованных более 2.
11. Всхожесть семян некоторого растения составляет 70%. Какова вероятность того, что из 100 посеянных семян взойдет не менее 80?
12. Книга в 500 страниц содержит 50 опечаток. Оценить вероятность того, что на случайно выбранной странице не менее 4 опечаток.
13. В ящике 100 деталей, из них 10 бракованных. Наудачу извлечены 4 детали. Найти вероятность того, что среди извлеченных деталей: а) нет бракованных; б) нет годных
14. На заводе рабочий за смену изготовляет n=625 деталей. Вероятность того, что деталь окажется 1 сорта равна р=0, 36. Какова вероятность того, что рабочий за смену изготовит: а) не менее k1=225, но не более k2=255 деталей 1 сорта; б) k=200 деталей 1-го сорта?
15. 90 % изделий данного предприятия – это продукция высшего сорта. Найти вероятность того, что из 600 приобретенных Вами изделии первого сорта будет от 500 до 550.
Задание 2.4. Числовые характеристики дискретной случайной величины
Решение типовых задач
Пример 2.4.1. При установившемся технологическом процессе предприятие выпускает 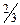 своих изделий первым сортом и
своих изделий первым сортом и 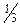 вторым сортом. Найти закон распределения случайной величины
вторым сортом. Найти закон распределения случайной величины 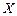 – числа изделий первого сорта из взятых наугад четырех изделий. Вычислить математическое ожидание
– числа изделий первого сорта из взятых наугад четырех изделий. Вычислить математическое ожидание  , дисперсию
, дисперсию  и среднее квадратическое отклонение этой случайной величины.
и среднее квадратическое отклонение этой случайной величины.
Решение. Очевидно, что случайная величина 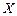 может принимать следующие возможные значения: 0, 1, 2, 3, 4. вероятности этих значений вычислим по формуле Бернулли:
может принимать следующие возможные значения: 0, 1, 2, 3, 4. вероятности этих значений вычислим по формуле Бернулли:
 ,
, 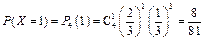 ,
,
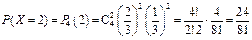 ,
, 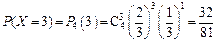 ,
, 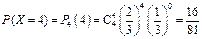 .
.
Проверка: 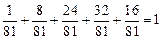 , т. е. вычисления выполнены правильно.
, т. е. вычисления выполнены правильно.
Итак, закон распределения случайной величины 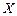 :
:

| |||||
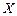
| 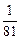
| 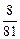
| 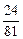
| 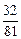
| 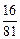
|
Вычислим математическое ожидание, дисперсию и среднее квадратическое отклонение:
 ;
;
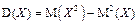
 ;
;
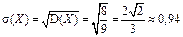 .
.
Пример 2.4.2. Дискретная случайная величина X задана рядом распределения:
| xi | -2 | |||
| pi | 0, 08 | 0, 40 | 0, 32 | 0, 2 |
Найти: а) математическое ожидание; б) дисперсию; в) среднее квадратическое отклонение случайной величины X; г) функцию распределения (найти и построить).
Решение:
а) Используя формулу, находим
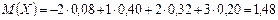 .
.
б) Дисперсию вычисляем по формуле (20):
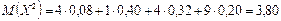 ,
, 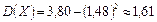 .
.
в) По формуле (21)  .
.
г) По определению функции распределения находим:
если  , то
, то 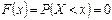 ;
;
если  , (например,
, (например,  ), то
), то 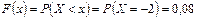 ;
;
если 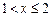 , (например,
, (например,  ), то
), то 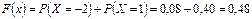 ;
;
если 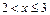 , то
, то 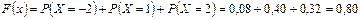 ;
;
если 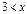 , то
, то 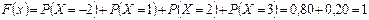 .
.
Итак, 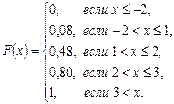
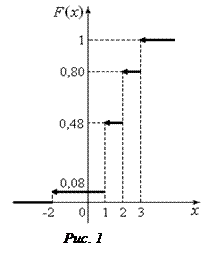
График функции 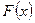 изображен на рисунке 1.
изображен на рисунке 1.
 |
Задачи для самостоятельного решения
2.4.1. Таблицей задан закон распределения дискретной случайной величины Х. Найти математическое ожидание М(Х), дисперсию D(X) и среднее квадратическое отклонение s(X).
| Вари-ант | Закон распределения | Вари-ант | Закон распределения | ||||||||||||||||||||
|
| ||||||||||||||||||||||
|
| ||||||||||||||||||||||
|
| ||||||||||||||||||||||
|
| ||||||||||||||||||||||
|
| ||||||||||||||||||||||
|
| ||||||||||||||||||||||
|
| ||||||||||||||||||||||
|
|
2.4.2. Найти закон распределения указанной дискретной СВ Х и ее функцию распределения F(X). Вычислить математическое ожидание M(X), дисперсию D(X) и среднее квадратичное отклонение σ (X). Построить график функции распределения F(X).
1. Производятся три выстрела по мишени. Вероятность поражения мишени первым выстрелом равна 0, 4, вторым – 0, 5, третьим – 0, 6. СВ Х – число поражений мишени.
2. Вероятность поражения цели при одном выстреле равна 0, 6. СВ Х – число поражений цели при четырех выстрелах.
3. Вероятность поступления вызова на АТС в течение 1 мин равна 0, 4; СВ Х – число вызовов, поступивших на АТС за 4 мин.
4. Вероятность успешной сдачи первого экзамена для студента равна 0, 9, второго – 0, 8, третьего – 0, 7. СВ Х – число сданных экзаменов.
5. Вероятность перевыполнения плана для СУ-1 равна 0, 9, для СУ-2 – 0, 8, для СУ-3 – 0, 7. СВ Х – число СУ, перевыполнивших план.
6. Вероятность попадания в цель при одном выстреле равна 0, 8; СВ Х – число попаданий в цель при трех выстрелах.
7. Вероятность выигрыша по одному билету лотереи равна 1/6; СВ Х – число выигрышных билетов из четырех.
8. В первой студенческой группе из 24 человек 4 отличника, во второй из 22 – 3 отличника, в третьей из 24 – 6 отличников и в четвертой из 20 – 2 отличника. СВ Х – число отличников, приглашенных на конференцию, при условии, что из каждой группы выделили случайным образом по одному человеку.
9. В партии из 15 телефонных автоматов 5 неисправных; СВ Х – число неисправных аппаратов среди трех случайным образом отобранных.
10. Вероятность сдачи данного экзамена для каждого из четырех студентов равна 0, 8; СВ Х – число студентов, сдавших экзамен.
11. В партии из 10 деталей имеется 8 стандартных. Из этой партии наудачу взято три детали. СВ Х – число стандартных деталей в выборке.
12. Из 25 контрольных работ, среди которых 5 оценены на 10 (десять) наугад извлекаются 3 работы. СВ Х – число работ, оцененных на 10 среди извлеченных.
13. В урне 5 белых и 20 черных шаров. Вынули три шара. СВ Х – число вынутых белых шаров.
14. Вероятность попадания мячом в корзину при каждом броске для данного баскетболиста равна 0, 4. СВ Х – число попаданий при четырех бросках.
15. СВ Х – число мальчиков в семье с пятью детьми, при равновероятном рождении мальчика и девочки.
Задание 2.5. Числовые характеристики непрерывной случайной величины