Решение типовых задач. Пример 2.5.1. По заданной функции распределения F(x) CB X найти плот­ность распределения и построить её график

Пример 2.5.1. По заданной функции распределения F(x) CB X найти плот­ность распределения и построить её график. Вычислить вероятность Р(а ≤ Х ≤ в) попадания значения СВ в заданный интервал, математическое ожидание и дисперсию.

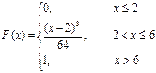
Решение. Плотность распределения определяется по формуле

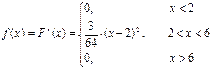
Искомая вероятность равна:

Математическое ожидание и дисперсия запишутся:

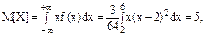
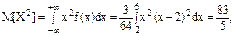
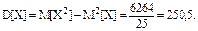
Пример 2.5.2. Дана плотность распределения случайной величины X:

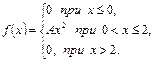
Найти: а) параметр A; б) математическое ожидание и дисперсию X; в) функцию распределения случайной величины X; г) построить график функ­ции распределения; д) найти вероятность попадания случайной величины X в интервал .

Решение:

а) Параметр A подберем так, чтобы выполнялось свойство плотности распределения: 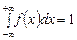. 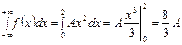, 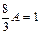. Отсюда .

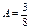б) Пользуясь формулой (22), получаем

.

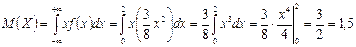Находим :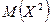

.

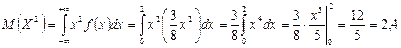Используя формулу (24), находим

.

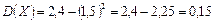в) Функцию распределения будем искать на каждом интервале от­дельно.

Для значений ,

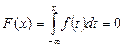Для значений .

Для значений .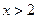

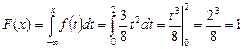Таким образом,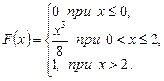

График этой функции изображен на рисунке 2.

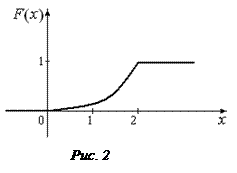
г) Вероятность попадания случайной величины X в интервал 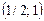вычис­ляем по формуле :

.