
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задание 2.6. Нормальный закон
|
|
Пример 2.6.1. Случайная величина X распределена по нормальному закону. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 30 и 10. Найти вероятность того, что X примет значение, принадлежащее интервалу (10, 50).
Решение. Воспользуемся формулой  .
.
В нашем случае, a =10, b =50, σ =10, μ =30. P(10< x < 50) = 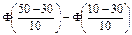 = 2Ф(2). Из таблицы находим Ф(2) = 0, 4772 и окончательно имеем P(10< x < 50) = 2·0, 4772 = 0, 9544.
= 2Ф(2). Из таблицы находим Ф(2) = 0, 4772 и окончательно имеем P(10< x < 50) = 2·0, 4772 = 0, 9544.
2.6.1. Найти вероятность попадания в заданный интервал [a, b] значения нормально распределенной случайной величины X, если известно её математическое ожидание M[X] и дисперсия D[X].
| Вар. | M [ X ] | D [ X ] | 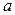
| b |
2.6.2.
1. Рост мужчины является случайной величиной, распределенной по нормальному закону с математическим ожиданием, равным 170 см, и дисперсией, равной 49 см2. Найти вероятность того, что трое наугад выбранных людей будут иметь рост от 170 до 175 см.
2. Рост лиц призывного возраста предполагается нормально распределенным с параметрами m = 172см и σ = 6см. Определить процент лиц - потенциальных танкистов (рост меньше 165см).
3. С.в. Y распределена по нормальному закону с математическим ожиданием, равным единице, и средним квадратическим отклонением, равным двум. Пусть X =3 Y. Найти вероятности  ,
, 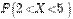 ,
, 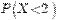 ,
, 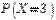 . Написать функции плотности и распределения для X и построить их примерные графики. Как выглядит для с.в. X правило «трех сигм»?
. Написать функции плотности и распределения для X и построить их примерные графики. Как выглядит для с.в. X правило «трех сигм»?
4. Автомат штампует детали. Контролируется длина х детали, которая распределена нормально, с математическим ожиданием 50 мм. Фактически длина детали не менее 32 мм и не более 68 мм. Найти вероятность того, что длина наудачу взятой детали: а) меньше 55 мм; б) лежит в интервале (34; 40).
5. Рост мужчин определенной возрастной группы распределен нормально с математическим ожиданием а=170 и среднеквадратическим отклонением s=4. Какую долю костюмов 3-го роста следует предусмотреть в общем объеме производства для данной возрастной группы, если 3-й рост определяется следующими пределами: 170-176
6. Автоматически фасуют сахар в пакеты по 1 кг. Реальный вес пакета X - случайная величина, распределенная по нормальному закону со средним квадратичным отклонением σ =5 г. Куплено 3 пакета сахара. Найти вероятность того, что хотя бы один из пакетов имеет отклонение от номинального веса не более 2 г
7. Случайная величина распределена нормально с математическим ожиданием 10. Вероятность попадания X в промежуток [0; 20] равна 0, 6. Найти вероятность попадания X в промежуток [0; 10].
8. Автомат штампует детали. Контролируется длина детали, которая распределена нормально с математическим ожиданием (проектная длина), равным 50 мм. Среднее квадратическое отклонение равно 3, 6 мм. Найти вероятность того, что отклонение длины изготовленной детали от проектной по абсолютной величине не превзойдет 5 мм.
9. Валик, изготовленный автоматом, считается стандартным, если отклонение его диаметра от проектного размера не превышает 2 мм. Случайные отклонения диаметров валиков подчиняются нормальному закону со средним квадратичным отклонением 1, 6 мм и математическим ожиданием, равным 0. Сколько стандартных валиков (в процентах) изготавливает автомат?
10. Рассеивание снарядов по дальности при стрельбе подчинено нормальному закону со среднеквадратичным отклонением σ =20 м. Определить вероятность разрушения блиндажа одним выстрелом, если перелет или недолет должны составить не более a =15 м
11. Дальность до объекта определяется дальномером, средняя квадратичная ошибка которого σ =10, систематическая ошибка +5 м. Ошибка измерения имеет нормальное распределение. Найти вероятность того, что измеренное значение не превзойдёт истинное более чем на 15 м.
12. Диаметр изготовляемых деталей является случайной величиной, распределенной по нормальному закону с параметрами a =14 и σ =3. Записать вид плотности вероятности случайной величины Z, построить ее график. Найти вероятность того, что размер диаметра наугад взятой для контроля детали окажется в заданном интервале 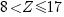 .
.
13. Детали, выпускаемые цехом, имеют диаметры, распределенные по нормальному закону с математическим ожиданием, равным 15 см, и дисперсией, равной 0, 55 см2. Найти вероятность того, что диаметр наугад взятой детали – от 12 до 18 см.
14. СВ Х распределена нормально с математическим ожиданием 80 и дисперсией 35. Вычислить вероятность попадания СВ Х в интервал (45; 95).
15. Автомат штампует детали. Контролируется длина Х, которая распределена по нормальному закону с математическим ожиданием (проектная длина) a =135 мм. Фактическая длина изготовленных деталей  мм. Найти вероятность того, что длина наудачу взятой детали меньше 136 мм. Какое отклонение длины детали от a можно гарантировать с вероятностью 0, 96? В каких пределах с вероятностью 0, 9973 будут заключены длины изготовленных деталей?
мм. Найти вероятность того, что длина наудачу взятой детали меньше 136 мм. Какое отклонение длины детали от a можно гарантировать с вероятностью 0, 96? В каких пределах с вероятностью 0, 9973 будут заключены длины изготовленных деталей?