Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
А. Отражение
|
|
Исследуем сначала поведение 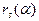 и
и 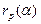 на границах отрезка
на границах отрезка 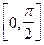 :
:
при 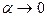 (просто положить
(просто положить 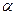 равным нулю нельзя, потому что будет неопределенность):
равным нулю нельзя, потому что будет неопределенность):
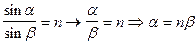
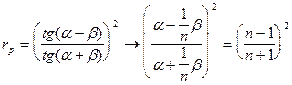
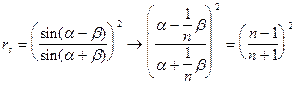
для случая падения из воздуха в стекло (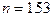 ):
): 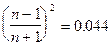
т.е. это величина порядка нескольких процентов (можно заметить, что если поменять среды местами - т.е. рассматривать падение из воды в воздух, то это значение не изменится)
В случае падения из оптически менее плотной среды в оптически более плотную при  :
:
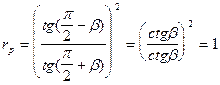
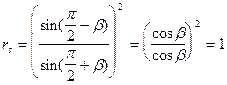
Действительно, преломленной волны при скользящем падении не образуется и интенсивность падающей волны не меняется.
В случае падения из оптически более плотной среды в оптически менее плотную, необходимо учесть явление полного внутреннего отражения, когда прошедшей волны нет - вся волна отражается от поверхности раздела. Это происходит при значениях 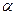 больших, чем
больших, чем 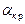 , вычисляемого следующим образом:
, вычисляемого следующим образом:
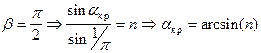 [1][к1]
[1][к1]
Для падения из стекла в воздух 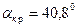
Здесь не рассматривается полное внутреннее отражение, поэтому  в случае падения из оптически более плотной среды в оптически менее плотную изменяется до
в случае падения из оптически более плотной среды в оптически менее плотную изменяется до  , в этом случае:
, в этом случае:
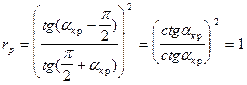
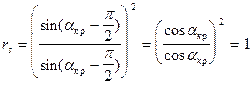
Далее исследуем поведение этих функций между крайними точками, для этого исследуем на монотонность функции: 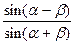 и
и 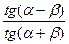
Нам понадобится производная 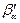 , найдем ее как производную функции, заданной неявно:
, найдем ее как производную функции, заданной неявно:
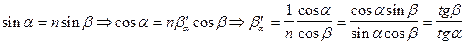
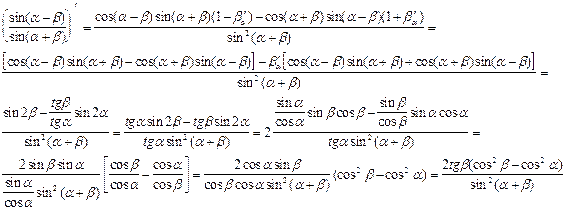 Знак этой производной (поскольку
Знак этой производной (поскольку  ,
,  ) зависит только от знака выражения
) зависит только от знака выражения 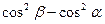 , это выражение > 0, когда
, это выражение > 0, когда 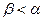 (то есть падение из оптически мене плотной среды в оптически более плотную) и < 0, когда
(то есть падение из оптически мене плотной среды в оптически более плотную) и < 0, когда 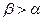 (из более оптически плотной в менее оптически плотную), следовательно в первом случае
(из более оптически плотной в менее оптически плотную), следовательно в первом случае 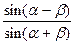 монотонно возрастает, а во втором, убывает. Но в случае
монотонно возрастает, а во втором, убывает. Но в случае 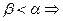
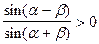 , следовательно по модулю это выражение будет возрастать, в случае
, следовательно по модулю это выражение будет возрастать, в случае 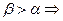
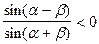 оно также будет по модулю возрастать. Таким образом,
оно также будет по модулю возрастать. Таким образом, 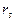 , как квадрат этого выражения, в обоих случаях монотонно возрастает от
, как квадрат этого выражения, в обоих случаях монотонно возрастает от 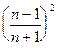 при
при 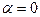 до 1 при
до 1 при 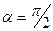 .или
.или 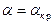 .
.
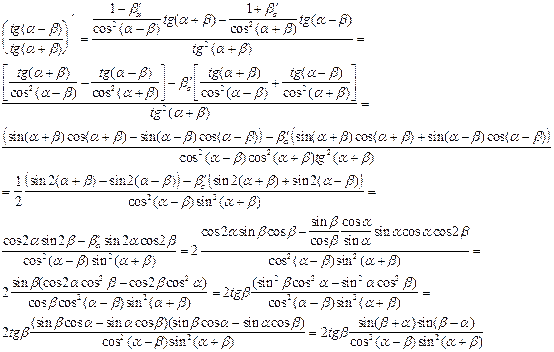
Знак этой производной, (поскольку 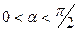 ,
,
есть > 0 при 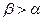 и < 0 при
и < 0 при 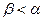 .
.
Знак функции 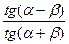 меняется следующим образом:
меняется следующим образом:
при 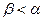 если
если 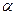 невелико
невелико 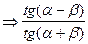 > 0, но эта функция проходит через нуль. Поскольку числитель, при рассматриваемых пределах изменения
> 0, но эта функция проходит через нуль. Поскольку числитель, при рассматриваемых пределах изменения 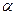 в 0 обращаться не может[2][к2] это происходит тогда, когда знаменатель обращается в бесконечность т.е.:
в 0 обращаться не может[2][к2] это происходит тогда, когда знаменатель обращается в бесконечность т.е.:
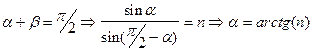
Это есть угол Брюстера (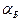 ), при котором
), при котором 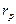 обращается в 0, то есть отраженная волна отсутствует. Для случая падения из воздуха в стекло
обращается в 0, то есть отраженная волна отсутствует. Для случая падения из воздуха в стекло 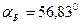 , для обратного случая (из стекла в воздух)
, для обратного случая (из стекла в воздух) 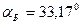 При переходе через этот угол
При переходе через этот угол 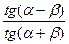 меняет знак на минус, следовательно
меняет знак на минус, следовательно 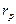 как квадрат этой функции сначала убывает (до нуля), а затем возрастает (до 1).
как квадрат этой функции сначала убывает (до нуля), а затем возрастает (до 1).
При 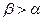 для небольших
для небольших 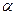
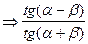 < 0, при переходе через
< 0, при переходе через 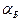 знак будет меняться на плюс. Переход через
знак будет меняться на плюс. Переход через 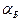 действительно будет иметь место, хотя
действительно будет иметь место, хотя 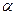 изменяется до
изменяется до 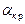 , а не до
, а не до 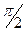 , поскольку
, поскольку 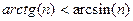 . Таким образом
. Таким образом  снова монотонно убывает до 0, а затем монотонно возрастает до 1.
снова монотонно убывает до 0, а затем монотонно возрастает до 1.
Итак, в обоих случаях  сначала монотонно убывает от
сначала монотонно убывает от 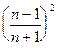 при
при 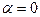 до 0 при
до 0 при 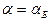 , а затем монотонно возрастает до 1 при
, а затем монотонно возрастает до 1 при 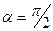 или
или 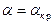 .
.
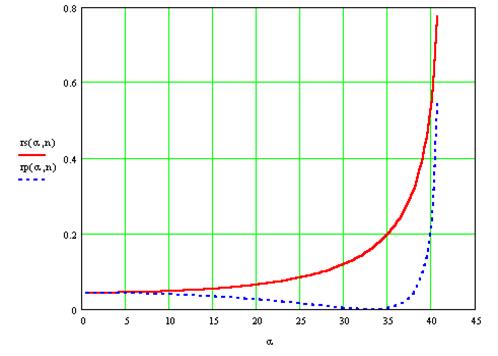
Полученные зависимости иллюстрируются следующими графиками:
на первом показана зависимость 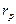 (сплошная линия) и
(сплошная линия) и 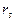 (пунктирная линия) от
(пунктирная линия) от 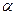 для случая падения волны из воздуха в стекло (n=1.51)
для случая падения волны из воздуха в стекло (n=1.51)

на втором -для случая падения волны из стекла в воздух