С. Набег фаз при отражении и преломлении

Из формул Френеля следует, что отношения , , 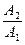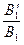и 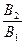могут в принципе получится и отрицательными. Поскольку амплитуда есть существенно положительная величина, в этом случае имеет место сдвиг фазы волны на 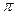. Далее выясним, когда такой сдвиг имеет место.

В случае отраженной p-волны 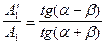, как установлено в п. А, эта функция

при n> 1 больше 0 при 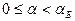и меньше 0 при 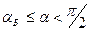, при n< 0 промежутки знакопостоянства меняются местами. Таким образом, в случае падения из менее оптически плотной среды в более плотную сдвиг фаз на 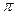в отраженной p-волне наблюдается при 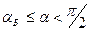, а в случае падения из более плотной в менее плотную - при .

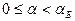В случае отраженной s-волны 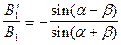, эта функция меньше 0 при и больше 0 в противном случае. Таким образом, сдвиг фаз на 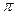в отраженной s-волне наблюдается при падении из менее оптически плотной среды в более плотную, и не наблюдается при падении из более плотной среды в менее плотную.

В случае произвольно падающей линейно поляризованной волны, которая представляется в виде суммы p и s-волн, в отраженной волне, таким образом, можно получить, в общем случае волну произвольной (эллиптической) поляризации.

Для исследования сдвига фаз в прошедшей волне, воспользуемся соотношениями, возникшими как промежуточные результаты при выводе (7) и (10):

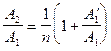и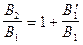

из этих соотношений видно, что, поскольку и 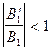, то всегда 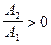и 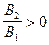. То есть, в прошедшей волне изменения фазы не происходит (причем это верно для волн произвольной поляризации).

[1] -здесь под n понимается показатель преломления той среды, куда падает луч относительно той, откуда он падает, в оптике в этом случае под n понимают показатель преломления оптически более плотной среды относительно оптически менее плотной, т.е. в этом случае в этой формуле стоит

[2]-- числитель также не может обращаться в бесконечность, поскольку это возможно только в случае, но в этом случае, а это невозможно т.к. и

[к1]

[к2]