
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Биномиальное распределение
|
|
Случайная величина X называется биномиально распределенной с параметрами n и p, если возможные значения  она принимает с вероятностями
она принимает с вероятностями  , вычисляемыми по формуле Бернулли:
, вычисляемыми по формуле Бернулли:
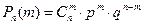 ,
, 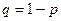 , где
, где 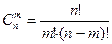 .
.
Пример 3. Вероятность попадания в цель при одном выстреле из орудия равна 0, 8. Производится три выстрела. Составить закон распределения случайной величины – числа попаданий в цель.
Решение. Дискретная случайная величина X – число попаданий в цель – распределена по биномиальному закону с параметрами 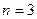 - число независимых испытаний (выстрелов) и
- число независимых испытаний (выстрелов) и  - вероятность попадания в цель при одном выстреле и может принимать значения
- вероятность попадания в цель при одном выстреле и может принимать значения  с вероятностями, вычисленными по формуле Бернулли:
с вероятностями, вычисленными по формуле Бернулли:




Проверка: 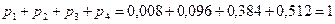 - верно.
- верно.
Закон распределения случайной величины X имеет вид:
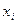
| ||||

| 0, 008 | 0, 096 | 0, 384 | 0, 512 |
