Числовые характеристики непрерывной случайной величины

Математическое ожидание и дисперсия непрерывной случайной величины X, возможные значения которой принадлежат всей числовой оси, вычисляются, соответственно, по формулам:

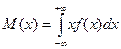, (13)

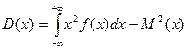. (14)

В частности, если все возможные значения непрерывной случайной величины X принадлежат интервалу , то формулы принимают вид:

,

.

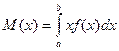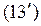
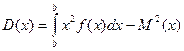Среднее квадратическое отклонение непрерывной случайной величины определяется так же, как и для дискретной случайной величины:

.

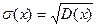Замечание. Следует заметить, что важнейшая характеристика положения – математическое ожидание – существует не для всех случайных величин. Можно составить примеры таких случайных величин, для которых математического ожидания не существует, так как соответствующая сумма или интеграл расходятся.

Пример 9. По заданной функции распределения 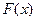найти функцию плотности 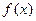, построить график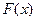и и 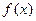, найти

.

Решение. Функцию плотности 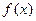находим по определению :

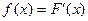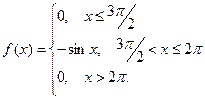
Строим графики функций 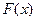(рис.5) и 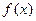(рис.6).

Рис. 5

Рис. 6

Пользуясь формулой , находим математическое ожидание случайной величины X:

=

Указанный интеграл вычисляем с помощью формулы интегрирования по частям:

.

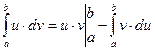В нашем случае:

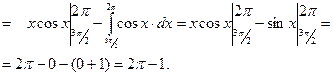
Пользуясь формулой 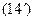, находим дисперсию случайной величины X:

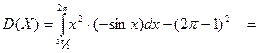
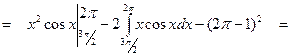
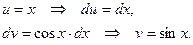
Тогда среднее квадратическое отклонение равно:

По формуле (8) вычисляем:

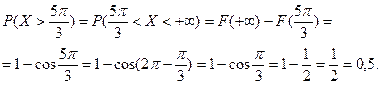
Пример 10. По заданной плотности распределения 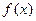найти функцию распределения 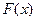, построить ее график и вычислить вероятность .

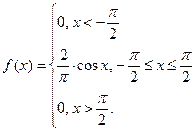
Решение. По формуле (11) находим:

Таким образом, функция распределения имеет вид:

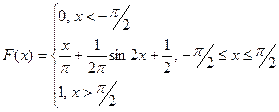
График функции 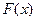изображен на рис. 7:

Рис. 7

Вычисляем вероятность:

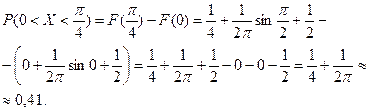
Пример 11. При каком значении параметра c функция 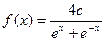является функцией плотности распределения некоторой случайной величины X на всей числовой оси?

Решение. Воспользуемся условием нормировки (12):

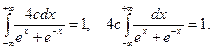
Вычислим несобственный интеграл:

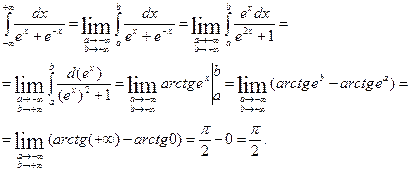
Получаем:

, откуда

Ответ: