
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Функция распределения случайной величины
|
|
Функцией распределения случайной величины X называется функция 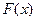 , которая для каждого значения аргумента x численно равна вероятности того, что при испытании случайная величина X примет значение, меньше чем x, т.е.:
, которая для каждого значения аргумента x численно равна вероятности того, что при испытании случайная величина X примет значение, меньше чем x, т.е.:
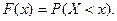 (7)
(7)
Функция распределения – самая универсальная характеристика случайной величины. Она существует для всех случайных величин: как дискретных, так и непрерывных. Функция распределения полностью характеризует случайную величину с вероятностной точки зрения, т.е. является одной из форм закона распределения.
Свойства функции распределения:
1. 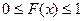
2. 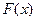 - неубывающая функция, т.е. при
- неубывающая функция, т.е. при 
 .
.
3. Вероятность попадания случайной величины на заданный интервал равна приращению функции распределения на этом интервале, т.е.:
 . (8)
. (8)
Замечание. Для непрерывной случайной величины вероятности 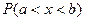 ,
, 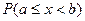 ,
, 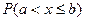 ,
, 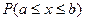 совпадают.
совпадают.
4. Используя функцию распределения, можно показать, что вероятность того, что непрерывная случайная величина X примет указанное строго определенное значение 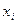 , равна нулю, т.е.
, равна нулю, т.е. 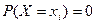 .
.
5. Если 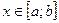 , то
, то 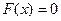 при
при  и
и 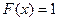 при
при  (иначе:
(иначе:  ,
,  ).
).