
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Графики функции распределения
|
|
1. Функция распределения непрерывной случайной величины всюду непрерывна, причем производная этой функции не имеет разрывов на всей числовой оси, за исключением конечного числа точек.
Если случайная величина X непрерывна, причем ее значения 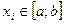 , то ее график имеет вид (рис. 2):
, то ее график имеет вид (рис. 2):

Рис. 2
2. Функция распределения дискретной случайной величины постоянна на интервалах, на которых нет ее значений, и имеет конечные разрывы (скачки) в точках, соответствующих ее значениям. Величины скачков равны вероятностям, с которыми случайная величина принимает свои значения.
Пример 8. Для дискретной случайной величины X из примера 1 найти и построить функцию распределения 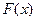 .
.
Решение. По определению функции распределения 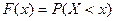 , используя полученный закон распределения случайной величины X, находим:
, используя полученный закон распределения случайной величины X, находим:
При 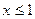
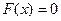 , т.к., например,
, т.к., например, 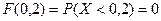 и так для всех точек данного интервала.
и так для всех точек данного интервала.
При 
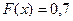 , т.к., например,
, т.к., например, 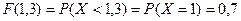 и так для всех точек данного интервала.
и так для всех точек данного интервала.
При 
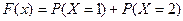 =
= 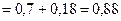 .
.
При 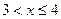
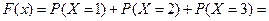
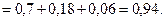
При 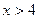
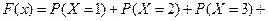
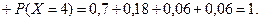
Таким образом, функция распределения будет такова:
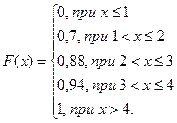
График функции распределения имеет вид (рис.3):

Рис. 3