Равномерное распределение

Непрерывная случайная величина X называется равномерно распределенной на интервале 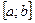, если ее плотность вероятности равна константе 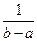на этом интервале и нулю вне его:

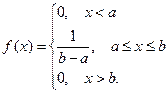
Примеры равномерно распределенных случайных величин:

1) время ожидания транспорта (автобуса, электрички) пассажиром;

2) ошибки при округлении чисел при расчетах.

Пример 12. Определить функцию распределения и числовые характеристики равномерно распределенной случайной величины.

Решение. По формуле (11) находим:

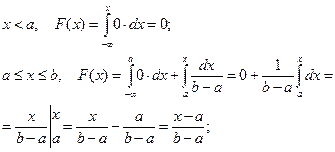
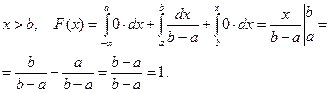
Получим:

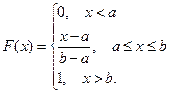
Учитывая, что 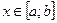, числовые характеристики вычисляются через определенные интегралы по формулам 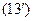и 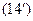, соответственно:

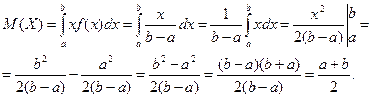
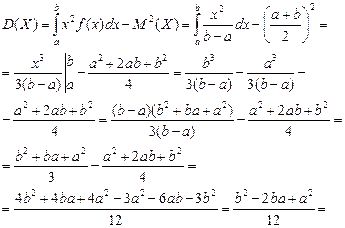
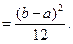
Таким образом, получили следующие формулы для вычисления числовых характеристик равномерно распределенной случайной величины:

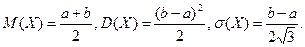(15)

Графики функции распределения 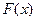(рис.8) и функции плотности 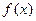(рис.9) имеют вид:

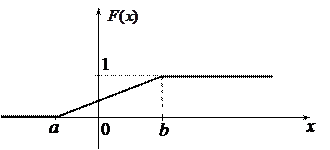
Рис. 8

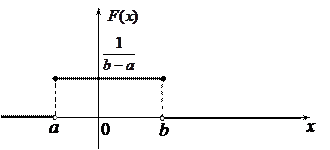
Рис. 9

Пример 13. Автобусы некоторого маршрута идут строго по расписанию. Интервал движения равен 25 мин. Найти вероятность того, что пассажир, случайно подошедший к остановке, будет ожидать очередной автобус более 15 мин. Найти математическое ожидание времени ожидания пассажиром автобуса.

Решение. Рассмотрим случайную величину X – время, отсчитанное от момента, в который очередной автобус только что отошел от остановки до момента, в который к остановке подошел пассажир. Случайная величина X равномерно распределена на интервале 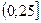. Тогда время T ожидания пассажиром очередного автобуса будет 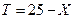. Требуется вычислить вероятность .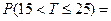

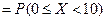Составим функцию распределения случайной величины X:

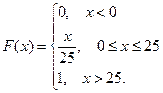
Тогда, пользуясь формулой (8), находим:

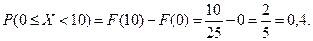
Вычисляем математическое ожидание:

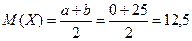мин.

Ответ: 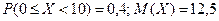мин.