Нормальное распределение. Непрерывная случайная величина X называется распределенной по нормальному закону, если ее плотность распределения вероятности имеет вид:

Непрерывная случайная величина X называется распределенной по нормальному закону, если ее плотность распределения вероятности имеет вид:

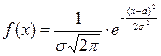, где 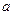- математическое ожидание и - средне квадратическое отклонение – параметры нормального распределения.

Нормальное распределение еще называют распределением Гаусса.

Примеры нормально распределенных случайных величин:

1) размеры механически обрабатываемых деталей;

2) ошибки всевозможных приборов;

3) производительность труда;

4) урожайность с/х культуры с 1га.

График плотности вероятности для нормального распределения представляет собой колокол-образную кривую (рис. 12); при этом параметр “a” соответствует точке максимума, через которую проходит ось симметрии, а параметр “ ” – расстоянию от этой оси до точки перегиба.

Рис. 12

Вероятность того, что случайная величина X, распределенная по нормальному закону, примет значение, принадлежащее интервалу , вычисляется по формуле:

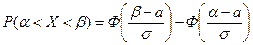, где (17)

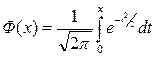- функция Лапласа, значения которой находятся по специальным таблицам в приложениях к учебникам.

Замечание 1. Особый интерес представляет частный случай: c какой вероятностью отклонение значений случайной величины X от математического ожидания по абсолютной величине не превосходит заданной величины :

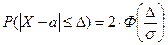. (18)

Замечание 2. Если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения. Такое событие происходит почти наверняка (правило “трех сигм”):

. (19)

Пример 16. Длина X изготавливаемой автоматом детали представляет собой случайную величину, распределенную по нормальному закону с параметрами 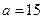см, 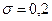см. Найти вероятность брака, если допустимые размеры детали должны быть см.

Решение. Требуется найти 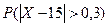- вероятность брака. Сначала находим вероятность изготовления качественной детали, используя формулу (18):

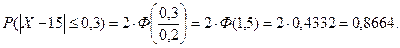Тогда искомая вероятность равна:

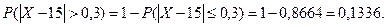
Ответ: 0, 1336.

Пример 17. Математическое ожидание дневной выручки торговой точки, нормально распределенной случайной величины X, равно 5 у.е. Найти вероятность того, что хотя бы в половине из четырех наугад выбранных дней случайная величина примет значение, не меньшее 6 у.е.

Решение. По условию задачи ,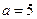

Сначала находи вероятность 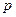того, что в один из дней случайная величина X примет значение, не меньшее 6 у.е. по формуле (17):

Тогда вероятность события A – “хотя бы в половине из четырех наугад выбранных дней случайная величина примет значение, не меньшее 6 у.е.” будет находиться с помощью формулы Бернулли для , , :

.

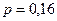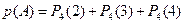Находим:

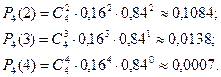
Получаем:

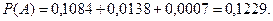
Ответ: 0, 1229.