Контрольное задание 4

4.1. - 4.6. Электрички некоторого маршрута идут строго по расписанию. Интервал движения равен T минут. Найти вероятность того, что пассажир, случайно подошедший к платформе, будет ожидать электричку менее t минут. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины – времени ожидания пассажиром электрички.

4.1. T =20, t =10. 4.2. T =30, t =10.

4.3. T =25, t =10. 4.4. T =30, t =5.

4.5. T =25, t =5. 4.6. T =20, t =8.

4.7. – 4.10. Случайная величина X – время безотказной работы прибора – распределена по показательному закону с параметром 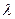. Найти вероятность того, что неисправность прибора наступит не ранее, чем через t часов. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X.

4.7. 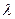=0, 02, t =100. 4.8. 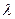=0, 02, t =50.

4.9. 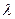=0, 01, t =100. 4.10. 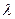=0, 03, t =100.

4.11. Случайная величина X – равномерно распределена на отрезке [2; 10]. Найти .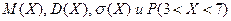

4.12. Для замера напряжений используются специальные тензодатчики. Определить среднюю квадратическую ошибку тензодатчика, если он ситематических ошибок не имеет, а случайные распределены по нормальному закону и с вероятностью 0, 8 не выходят за пределы 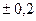мк.

4.13. Математическое ожидание нормально распределенной случайной величины равно 10, а дисперсия 4. Найти вероятность того, что в результате испытания случайная величина примет значение из интервала (12; 14).

4.14. Производится измерение диаметра вала без систематических ошибок. Случайные ошибки X подчинены нормальному закону с 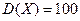мм. Найти .

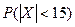4.15. Ошибка измерения дальности подчинена нормальному закону с систематической ошибкой a =20 м и средним квадратическим отклонением =40 м. Найти вероятность того, что измеренное значение дальности будет отклоняться от истинного не более, чем на 30 м.

4.16. Случайная величина X – равномерно распределена на отрезке [10; 20]. Найти .

4.17. Станок – автомат изготавливает валики, причем контролирует их размеры X. Считая, что X – нормально распределенная случайная величина с математическим ожиданием a =10 мм и средним квадратическим отклонением 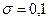мм, найти симметричный интервал, в котором с вероятностью 0, 9973 будут заключены диаметры изготавливаемых валиков.

4.18. Случайная величина X распределена нормально с математическим ожиданием a =10. Вероятность попадания X в интервал (10; 20) равна 0, 3. Чему равна вероятность попадания X в интервал (0; 10)?

4.19. Случайные значения веса зерна распределены нормально с параметрами a =0, 15 г и г. Определить величину, которую не превзойдет вес отдельного зерна с вероятностью 0, 99.

4.20. Случайная величина X равномерно распределена на отрезке [0; 1]. Найти и вероятность того, что в четырех независимых испытаниях случайная величина X попадет на интервал [0; 0, 5] три раза.

4.21. Случайные ошибки измерения подчинены нормальному закону со средним квадратическим отклонением 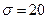мм и математическим ожиданием a =0. Найти вероятность того, что из трех независимых измерений, ошибка хотя бы одного не превзойдет по абсолютной величине 4 мм.

4.22. Длина детали представляет собой нормально распределенную случайную величину с математическим ожиданием 40 мм и средним квадратическим отклонением 3 мм. Найти вероятность того, что длина произвольно взятой детали будет больше 34 мм, но меньше 43 мм.

4.23. В условиях задачи 4.22. найти вероятность того, что длина детали отклонится от ее математического ожидания не более, чем 1, 5 мм.

4.24. Случайная величина X равномерно распределена на отрезке [5; 10]. Найти и вероятность того, что в трех независимых испытаниях случайная величина X попадет на интервал [6; 8] не менее одного раза.

4.25. Случайная величина X равномерно распределена на отрезке [2; 6]. Найти и вероятность того, что в четырех независимых испытаниях случайная величина X попадет на интервал [3; 5] два раза.

Литература

1. Вентцель, Е.С. Задачи и упражнения по теории вероятностей / Е.С. Вентцель, Л.А. Овчаров. – М.: Высшая школа, 2000. – 366 с.

2. Сборник задач по теории вероятностей, математической статистике и теории случайных функций/ под ред. А.А. Свешникова. – М.: Наука, 1970.

3. Данко, П.Е. Высшая математика в упражнениях и задачах. Ч. 3/ П.Е. Данко, А.Г. Попов. – М.: Высшая школа, 1971. – 288 с.

4. Вентцель, Е.С. Теория вероятностей / Е.С. Вентцель. – М.: Физматгиз, 1958. – 464 с.

5. Гмурман, В.Е. Руководство к решению задач по теории вероятностей и математической статистике / В.Е. Гмурман. – М.: Высшая школа, 2001.

6. Захаров, В.К. Теория вероятностей / В.К. Захаров, Б.А. Севастьянов, В.П. Чистяков.– М.: Наука, 1983. – 160 с.

7. Виленкин, Н.Я. Задачник-практикум по теории вероятностей с элементами комбинаторики и математической статистики/ Н.Я. Виленкин, В.Г. Потапов. – М.: Просвещение, 1979. – 112 с.

8. Лютикас, В.С. Факультативный курс по математике: теория вероятностей/ В.С. Лютикас. – М.: Просвещение, 1990. – 160 с.

Содержание

1. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ... 3

1.1. Закон распределения вероятностей дискретной случайной величины.. 3

1.2. Биномиальное распределение. 7

1.3. Распределение Пуассона. 8

1.4. Математические операции над дискретными случайными величинами. 9

1.5. Числовые характеристики дискретной случайной величины.. 11

Контрольное задание 1. 16

Контрольное задание 2. 19

2. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ... 23

2.1. Функция распределения случайной величины.. 24

2.2. Плотность распределения вероятностей непрерывной случайной величины 27

2.3. Числовые характеристики непрерывной случайной величины.. 28

2.4. Равномерное распределение. 34

2.5. Показательное распределение. 38

2.6. Нормальное распределение. 41

Контрольное задание 3. 43

Литература. 50

Бесклубная Антонина Вячеславовна,

Павел Валерьевич Столбов