
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Показательное распределение
|
|
Непрерывная случайная величина X называется распределенной по показательному закону, если ее плотность распределения вероятности имеет вид:
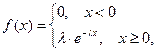
где 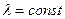 ,
, 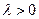 - параметр распределения.
- параметр распределения.
Функция распределения показательного распределения имеет вид:
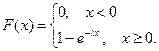
Графики функции распределения 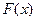 и функции плотности
и функции плотности 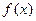 представлены на рис. 10 и рис. 11, соответственно.
представлены на рис. 10 и рис. 11, соответственно.
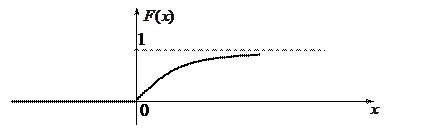
Рис. 10
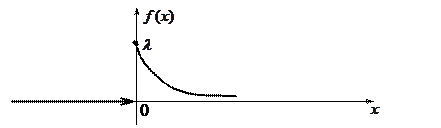
Рис. 11
Числовые характеристики случайной величины, распределенной по показательному закону, вычисляются по формулам:
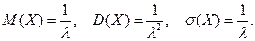 (16)
(16)
К показательному распределению приводят задачи о длительности безаварийной работы различных машин и приборов, оно играет особую роль в теории массового обслуживания и надежности, в страховом деле, демографии и многих других прикладных дисциплинах.