Задача 6 практика 2

Задача 4.11. Квантовый гармонический осциллятор с частотой колебаний 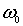находится в первом возбужденном состоянии. Найдите средние значения потенциальной 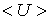и кинетической 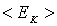энергий осциллятора.

Решение: В силу того, что осциллятор находится в первом возбужденном состоянии, его энергия, согласно (4.81), равна 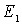= 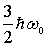, а соответствующая ему волновая функция имеет вид (4.85)

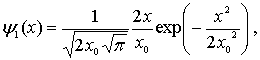
где .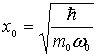

Операторы потенциальной 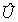и кинетической 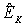энергий в рассматриваемой задаче есть

Согласно (3.62), средние значения потенциальной 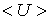и кинетической 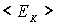энергий осциллятора в состоянии, описываемом волновой функцией 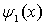, определяются выражениями

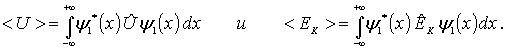
Найдем среднее значение потенциальной энергии гармонического осциллятора

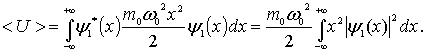
С учетом явного вида волновой функции 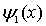получаем

где 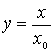. Поскольку функция, стоящая под знаком интеграла, является четной, то

где интеграл 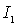= = 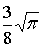. Таким образом, среднее значение потенциальной энергии гармонического осциллятора в первом возбужденном состоянии равно

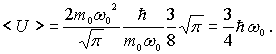
Найдем теперь среднее значение кинетической энергии

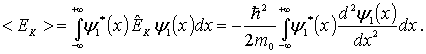
Вторая производная волновой функции по координате равна

Подставляя 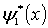и 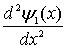в выражение для 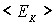, получаем

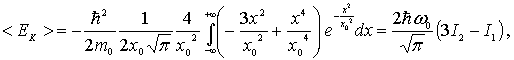
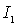где интеграл = = . Подставляя и в выражение для , получаем

Таким образом, мы показали, что для первого возбужденного состояния гармонического осциллятора средние значения потенциальной энергии 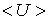и кинетической энергии 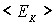равны между собой и составляют половину полной энергии осциллятора 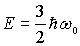. Можно показать, что это утверждение будет справедливым и для любого другого состояния квантового гармонического осциллятора. Полученный результат подтверждает вывод, сделанный в разделе 2.3, о том, что в квантовой механике равенство полной энергии частицы сумме ее потенциальной и кинетической энергий выполняется только для средних значений энергии.