Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Частные подстановки
|
|
1. Если  – нечетная функция относительно
– нечетная функция относительно 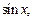 т. е.
т. е.  то подынтегральное выражение приводится к рациональной функции подстановкой
то подынтегральное выражение приводится к рациональной функции подстановкой 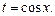
2. Если  – нечетная функция относительно
– нечетная функция относительно  т. е.
т. е.  то подынтегральное выражение приводится к рациональной функции подстановкой
то подынтегральное выражение приводится к рациональной функции подстановкой 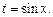
3. Если  – четная функция относительно
– четная функция относительно 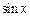 и
и  т. е.
т. е.  то подынтегральное выражение приводится к рациональной функции подстановкой
то подынтегральное выражение приводится к рациональной функции подстановкой 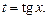
4. Интеграл 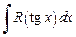 приводится к рациональной функции с помощью подстановки
приводится к рациональной функции с помощью подстановки 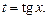
5. Интеграл  приводится к рациональной функции с помощью подстановки
приводится к рациональной функции с помощью подстановки 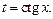
Пример 1. Найти неопределенный интеграл:
1)  2)
2) 
Решение. 1) Заменяя произведение  по формуле (19.22), получаем:
по формуле (19.22), получаем:
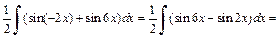
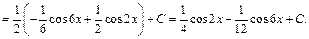
2) Интеграл 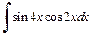 также можно вычислить, преобразуя произведение тригонометрических функций в сумму. Используем иной способ:
также можно вычислить, преобразуя произведение тригонометрических функций в сумму. Используем иной способ:
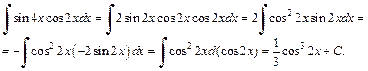
Пример 2. Найти неопределенный интеграл:
1)  2)
2) 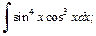 3)
3) 
Решение. 1) Показатель степени синуса – нечетное натуральное число. Поэтому в подынтегральной функции выделим первую степень синуса:


Получаем:

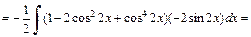

Интегрируя как степенную функцию относительно  получаем:
получаем:
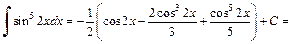
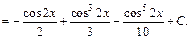
2) В подынтегральной функции выделим степень косинуса:
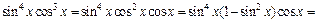
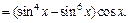
Получим:
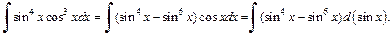
Интегрируя как степенную функцию относительно 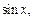 получаем:
получаем:
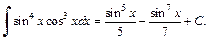
3) Поскольку  то имеем:
то имеем:

Применим подстановку 

Возвращаемся к старой переменной. Заменяем t на 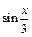 и получаем:
и получаем:
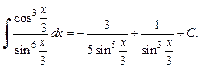
Пример 3. Найти неопределенный интеграл:
1)  2)
2) 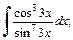
3) 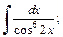 4)
4) 
Решение. 1) Показатель степени синуса  показатель степени косинуса
показатель степени косинуса 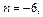
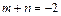 – четное отрицательное число. Так как в числителе находится степень синуса, то применим подстановку
– четное отрицательное число. Так как в числителе находится степень синуса, то применим подстановку 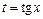 и используем формулы (19.24). Получаем:
и используем формулы (19.24). Получаем:
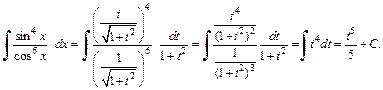
Заменив t на 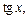 окончательно получаем:
окончательно получаем:

2) Показатель степени синуса 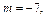 показатель степени косинуса
показатель степени косинуса 
 – четное отрицательное число. Так как в числителе находится степень косинуса, то удобнее применить подстановку
– четное отрицательное число. Так как в числителе находится степень косинуса, то удобнее применить подстановку


Используя формулы (19.25), получаем:
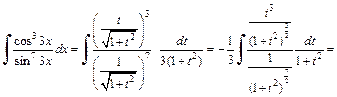

Заменив t на 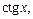 получаем:
получаем:
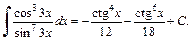
3) 1-й способ. Показатель степени синуса 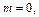 показатель степени косинуса
показатель степени косинуса 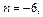
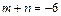 – четное отрицательное число. Применим подстановку
– четное отрицательное число. Применим подстановку 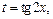 тогда
тогда 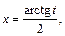
 Используя формулы (19.24), получаем:
Используя формулы (19.24), получаем:

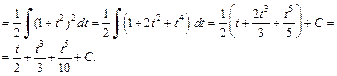
Заменяем t на 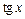 и получаем:
и получаем:
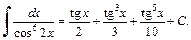
2-й способ. Преобразуем подынтегральное выражение и применим формулы (19.26):
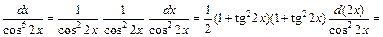
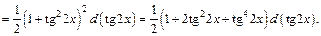
Интегрируя как степенную функцию относительно 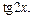 получаем:
получаем:
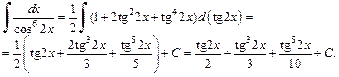
4) Имеем 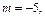

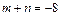 – четное отрицательное число. Применим подстановку
– четное отрицательное число. Применим подстановку 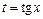 и формулы (19.24), получаем:
и формулы (19.24), получаем:
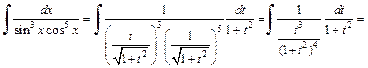

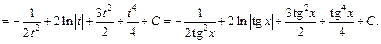
Пример 4. Найти неопределенный интеграл:
1) 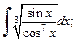 2)
2) 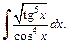
Решение. 1) Показатель степени синуса 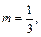 показатель степени косинуса
показатель степени косинуса 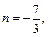
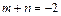 – четное отрицательное число. Применив подстановку
– четное отрицательное число. Применив подстановку 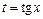 и формулы (19.24), получаем:
и формулы (19.24), получаем:
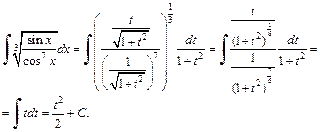
Возвращаемся к старой переменной. Заменяя t на 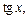 получаем:
получаем:

2) Преобразуем подынтегральную функцию к виду
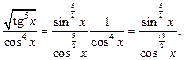
Имеем 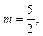
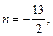
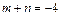 – четное отрицательное число. Применив подстановку
– четное отрицательное число. Применив подстановку 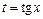 и формулы (19.24), получаем:
и формулы (19.24), получаем:
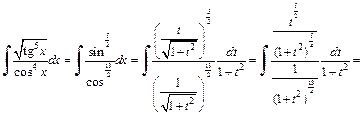

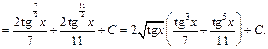
Пример 5. Найти неопределенный интеграл:
1) 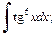 2)
2) 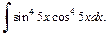
Решение. 1) 1-й способ. Применяя подстановку 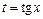 и формулы (19.24), получаем:
и формулы (19.24), получаем:
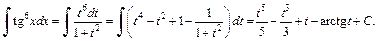
Заменяем t на tg x:
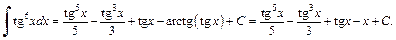
2-й способ. Представив подынтегральную функцию в виде  и применив формулу (19.26), получаем:
и применив формулу (19.26), получаем:
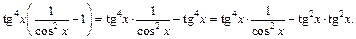
Еще два раза применим формулу (19.26):
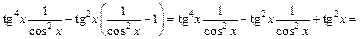
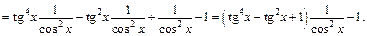
Учитывая, что 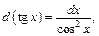 получим интеграл от рациональной функции относительно
получим интеграл от рациональной функции относительно 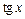
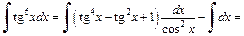
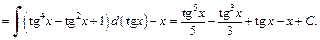
2) Имеем интеграл вида (19.23). Используя формулу (19.29), получаем:

Далее, понижая степень по формуле (19.27), имеем:

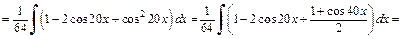
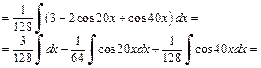
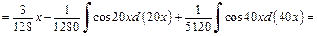
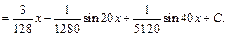
Пример 6. Найти неопределенный интеграл:
1) 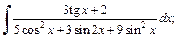 2)
2) 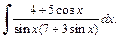
Решение. 1) Запишем подынтегральную функцию

Так как подынтегральная функция является четной по sin x и cos x, т. е. 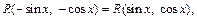 то применим подстановку
то применим подстановку 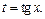 Вначале умножим и поделим знаменатель подынтегрального выражения на
Вначале умножим и поделим знаменатель подынтегрального выражения на 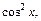 получаем:
получаем:
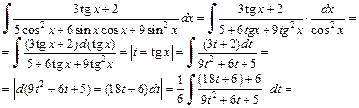

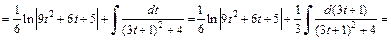
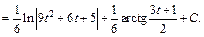
Возвращаемся к заданной переменной, заменяем t на tg x и приходим к ответу: 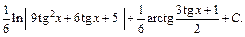
2) Поскольку подынтегральная функция не является нечетной ни по sin x, ни по cos x, то применим универсальную тригонометрическую подстановку 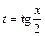 и формулы (19.30). Получаем:
и формулы (19.30). Получаем:

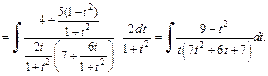
Разложив подынтегральную функцию на сумму простейших дробей, сводим заданный интеграл к разности двух интегралов, которые вычисляем:

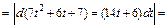

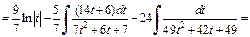
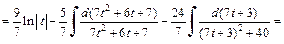
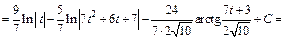

Заменяя t на 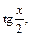 приходим к ответу:
приходим к ответу: