Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тригонометрическая подстановка
|
|
Интегралы вида

где R – некоторая рациональная функция относительно x и 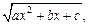 могут быть вычислены с помощью тригонометрических подстановок, которые приводят его к интегралу от рациональной функции.
могут быть вычислены с помощью тригонометрических подстановок, которые приводят его к интегралу от рациональной функции.
В квадратном трехчлене выделим полный квадрат 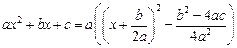 и применим подстановку
и применим подстановку  В результате под корнем получим одно из 3-х выражений:
В результате под корнем получим одно из 3-х выражений: 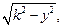
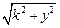 или
или 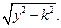
Если имеем 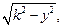 то для уничтожения иррациональности применим подстановку
то для уничтожения иррациональности применим подстановку  в результате которой
в результате которой 
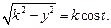 Аналогично можно использовать подстановку
Аналогично можно использовать подстановку 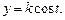
Если имеем  то для уничтожения иррациональности применяется подстановка
то для уничтожения иррациональности применяется подстановка 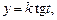 в результате которой имеем:
в результате которой имеем: 

Если под интегралом есть выражение  то подставляем
то подставляем 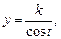 т. е.
т. е. 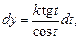

Далее интеграл вычисляют как интеграл от тригонометрической функции и возвращаются к старой переменной, выражая последовательно t через y и x.
Пример 1. Найти неопределенный интеграл:
1) 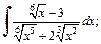 2)
2) 
3)  4)
4) 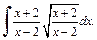
Решение. 1) Поскольку интеграл имеет вид: 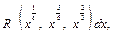 а
а 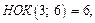 то применим подстановку
то применим подстановку  Тогда
Тогда
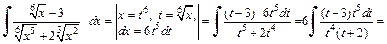
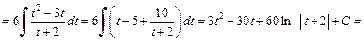
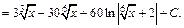
2) Интеграл имеет вид: 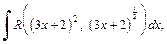 поэтому применим подстановку
поэтому применим подстановку 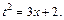 Тогда имеем:
Тогда имеем:

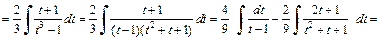
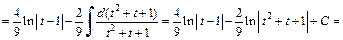
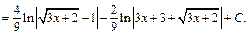
3) Интеграл имеет вид: 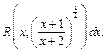
Применим подстановку 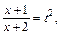

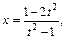
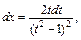
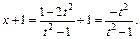
Получаем: 
4) Интеграл имеет вид: 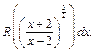
Применим подстановку 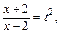
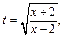

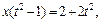
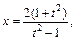
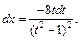
Получаем интеграл
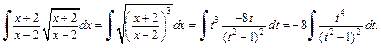
Для вычисления последнего интеграла вместо разложения на простейшие дроби применим формулу интегрирования по частям. Положим:
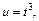


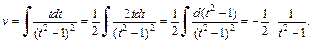
Получаем:
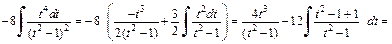

Заменяем t на  тогда имеем:
тогда имеем:

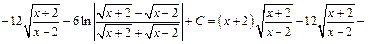
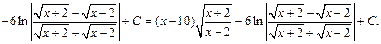
Пример 2. Найти неопределенный интеграл:
1) 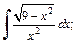 2)
2) 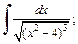 3)
3) 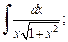 4)
4) 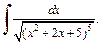
Решение. 1) Положим 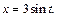
Тогда 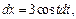
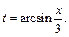
Интеграл примет вид:

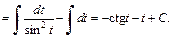
Возвращаемся к заданной переменной, заменяем t на 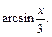 Тогда
Тогда 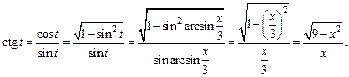
Приходим к ответу: 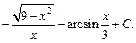
2) Применим подстановку 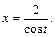
Тогда 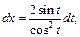

Получаем интеграл
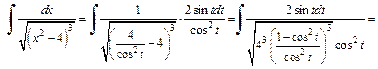
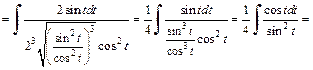
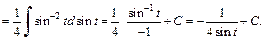
Заменяя t на 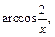 получаем:
получаем:
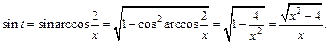
Приходим к ответу: 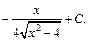
3) 1-й способ. Применим подстановку 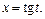
Тогда 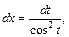
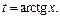
Интеграл примет вид:
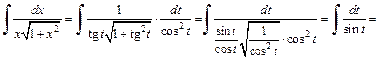
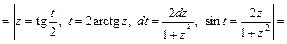

Заменяем t на 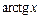 и применяем формулу
и применяем формулу 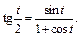
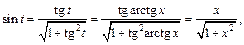
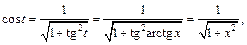

Приходим к ответу:
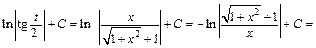
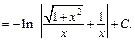
2-й способ. Применим подстановку 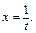 Тогда
Тогда 
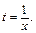 Получаем интеграл
Получаем интеграл
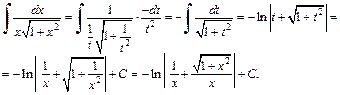
4) Выделим полный квадрат в квадратном трехчлене 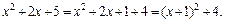 Положим
Положим 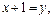 тогда
тогда  получаем интеграл
получаем интеграл 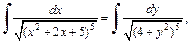 для вычисления которого применим тригонометрическую подстановку
для вычисления которого применим тригонометрическую подстановку 
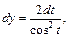

Тогда имеем:

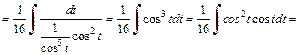
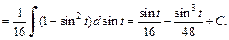
Заменяем 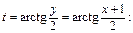
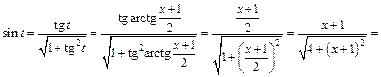
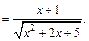
Приходим к ответу: