Екстремум функції

Означення 2.1. Точка 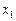називається точкою максимуму функції 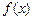, якщо в деякому околі точки 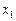виконується нерівність 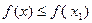(рис. 4).

Означення 2.2. Точка називається точкою мінімуму функції 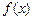, якщо в деякому околі точки справджується нерівність 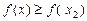(рис. 4).
Точки максимуму і мінімуму називаються точками екстремуму функції, а значення функції у точках 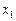і – відповідно максимумом і мінімумом функції. Максимум і мінімум функції об’єднуються під загальною назвою екстремуму функції, який часто називають локальним екстремумом, підкреслюючи, що поняття екстремуму пов’язане з достатньо малим околом точки екстремуму. Це означає на одному проміжку функція може мати декілька точок максимуму і мінімуму.

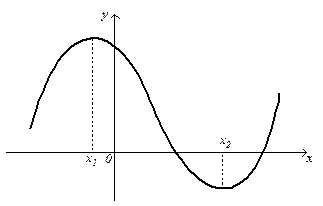
Рис. 4. Екстремуми функції

Теорема 2.1. (необхідна умова екстремуму). Якщо функція 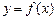має в точці 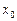екстремум, то її похідна в цій точці дорівнює нулеві 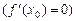або не існує

Іншими словами, функція 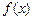може мати екстремум тільки у тих точках, в яких похідна дорівнює нулеві або не існує. Точки, в яких похідна функції дорівнює нулеві або не існує, називаються критичними (або стаціонарними) точками. Звертаємо увагу на те, що ці точки повинні входити в область визначення функції. Однак легко переконатись, що критична точка зовсім не обов’язково є точкою екстремуму. Наприклад, функція 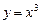зростає на усій числовій осі (див. додаток). Похідна в точці 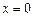дорівнює нулеві, тобто 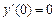, але екстремуму в цій точці немає.
Отже, щоб знайти екстремуми функції, потрібно додатково досліджувати критичні точки. Іншими словами, необхідно визначити достатню умову екстремуму.
Теорема 2.2. (перша достатня умова екстремуму). Якщо, переходячи через точку 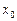, похідна диференційованої функції 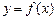змінює знак з плюса на мінус, то точка 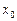є точкою максимуму функції 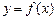, а якщо з мінуса на плюс, то 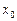– точка мінімуму.

Схема дослідження функції на екстремум.
1. Знайти область визначення функції .
2. Обчислити похідну .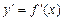
3. Визначити критичні точки функції, тобто точки, в яких 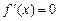або не існує.
4. Дослідити знак похідної ліворуч і праворуч від кожної критичної точки і зробити висновок про наявність екстремумів функції.
5. Знайти екстремуми функції, обчисливши значення функції в точках екстремуму.

Приклад 2.1. Дослідити на екстремум функцію .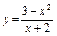
á 1. Область визначення цієї функції .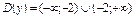
2.Обчислюємо похідну функції .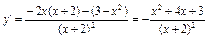
3. Прирівнюємо похідну до нуля і знаходимо критичні точки функції:
.
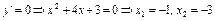Зауважимо, що в точці 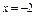похідна 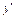не існує, але ця точка не є критичною, оскільки вона не входить в область визначення функції.
4. На числову вісь наносимо область визначення функції і критичні точки (рис.5).

Рис. 5. Інтервали монотонності

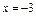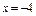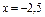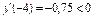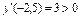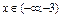Щоб встановити знак похідної ліворуч і праворуч від критичної точки виберемо, наприклад, значення і і знайдемо і ; отже, , якщо і 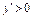, якщо .
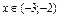Аналогічно встановлюємо, що 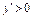на інтервалі 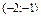і , якщо .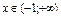
Згідно з достатньою умовою 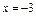– точка мінімуму цієї функції, а – точка максимуму.
5. Знаходимо , .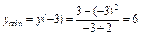
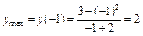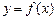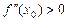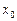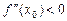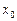Теорема 2.3. (друга достатня умова екстремуму). Якщо функція двічі диференційована і , а , то є точкою мінімуму функції; якщо , то є точкою максимуму.

Схема дослідження на екстремум функції 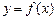за допомогою другої достатньої умови загалом аналогічна до наведеної вище схеми. Відмінність в п. 4, який встановлює наявність екстремуму: тут необхідно знайти другу похідну 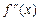і визначити її знак у кожній критичній точці.

Приклад 2.2. Функції, що описують залежність загального доходу і загальних витрат 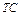фірми від кількості одиниць 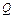продукції, мають вигляд: 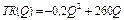(гр.од.) і 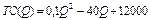(гр.од.). Знайти обсяг 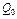продукції, який максимізує прибуток, і максимальний прибуток.
á Функція прибутку – це різниця між функціями загального доходу і загальних витрат, тобто
.
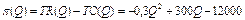Значення 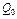, яке максимізує прибуток, є точкою максимуму функції прибутку . Знайдемо критичні точки цієї функції:
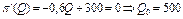– критична точка.
Оскільки 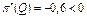, то функція , якщо 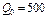, має максимум; 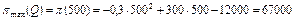(гр.од.).