Опуклість і увігнутість функції. Точки перегину

Означення 4.1. Функція 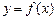називається опуклою (опуклою вгору) на інтервалі 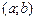, якщо для довільних двох точок 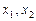з цього проміжку відрізок, що з’єднує точки 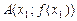і , розміщений під графіком цієї функції (рис. 7).

Означення 4.2. Функція 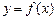називається увігнутою (опуклою вниз) на інтервалі 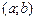, якщо для довільних двох точок 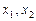з цього проміжку відрізок, що з’єднує точки і , розташований над графіком цієї функції (рис. 8).

Рис. 7.Опукла функція Рис. 8. Увігнута функція

Теорема 4.1. (достатня умова опуклості та увігнутості функції). Нехай функція 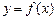двічі диференційована на інтервалі 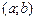. Тоді:
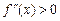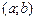1)якщо на , то функція увігнута на цьому інтервалі;
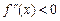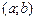2) якщо на , то функція опукла на цьому інтервалі.
Означення 4.3. Точкою перегину графіка неперервної функції називається точка, яка відокремлює інтервали, на яких функція опукла і увігнута.

Теорема 4.2. (ознака точки перегину). Якщо 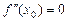і 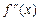, переходячи через точку 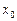, змінює знак, то 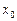є точкою перегину графіка функції .

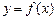Приклад 4.1. Визначити інтервали опуклості та увігнутості, точки перегину графіка функції .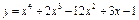
á Знайдемо другу похідну :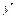
, .
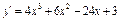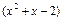Корені рівняння 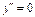– 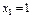та .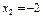
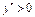на інтервалах 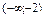і 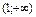, отже, на цих інтервалах функція увігнута;

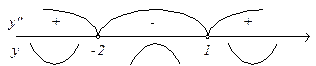
Рис. 9. Точки перегину функції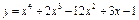

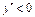на інтервалі 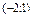, отже, функція на ньому опукла, а 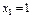і 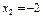є точками перегину (рис. 9). Значення функції в точках перегину .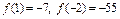