
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Диференціал функції. Основні властивості диференціала
|
|
Приріст  диференційованої функції
диференційованої функції  можна подати у вигляді
можна подати у вигляді 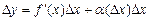 , де
, де 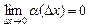 .
.
Перший доданок 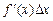 є головною частиною приросту функції, лінійною щодо
є головною частиною приросту функції, лінійною щодо 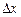 .
.
Означення 7.1. Головна, лінійна щодо 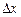 , частина приросту
, частина приросту  диференційовної функції
диференційовної функції 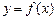 називається диференціалом цієї функції і позначається символом
називається диференціалом цієї функції і позначається символом 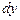 або
або 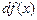 .
.
Геометричний зміст диференціала: диференціал 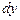 є приростом ординати дотичної, проведеної до кривої в точці
є приростом ординати дотичної, проведеної до кривої в точці 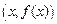 , що відповідає приросту аргументу
, що відповідає приросту аргументу 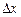 (рис. 15).
(рис. 15).
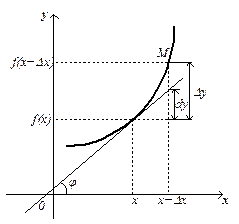
Рис. 15. Геометричний зміст диференціала функцій
Згідно з означенням 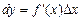 . Якщо
. Якщо 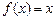 , то
, то 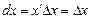 , тобто диференціал
, тобто диференціал 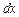 незалежної змінної
незалежної змінної 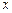 збігається з її приростом
збігається з її приростом 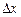 . Тому формулу для диференціала функції можна записати у вигляді
. Тому формулу для диференціала функції можна записати у вигляді
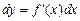 .
.
Властивості диференціала загалом аналогічні до властивостей похідної (тут 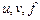 – диференційовані функції,
– диференційовані функції, 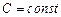 ):
):
1. 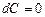 ; 4.
; 4.  ;
;
2. 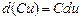 ; 5.
; 5. 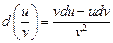 ;
;
3. 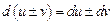 ; 6.
; 6. 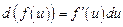 .
.
Зауважимо, що властивість 6 виражає інваріантність форми диференціала незалежно від того, чи змінна  є незалежною, чи функцією іншої змінної.
є незалежною, чи функцією іншої змінної.