Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Зростання і спадання функцій. Нагадаємо, що функція називається зростаючою (спадною) на інтервалі , якщо для довільних , якщо виконується нерівність .
|
|
Нагадаємо, що функція  називається зростаючою (спадною) на інтервалі
називається зростаючою (спадною) на інтервалі 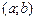 , якщо для довільних
, якщо для довільних  , якщо
, якщо 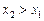 виконується нерівність
виконується нерівність 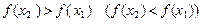 .
.
Теорема 1.1. (достатня умова монотонності). Припустимо, що функція 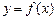 диференційована на
диференційована на 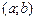 . Якщо
. Якщо  для всіх
для всіх 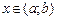 , то
, то 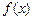 – зростаюча на
– зростаюча на 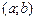 ; якщо
; якщо 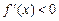 для всіх
для всіх 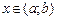 , то
, то 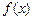 – спадна на
– спадна на 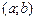 .
.
Зауваження. Якщо 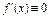 на
на 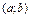 , то
, то  стала на
стала на 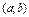 .
.
.
Геометрична інтерпретація умови монотонності функції наведена на рис. 1.
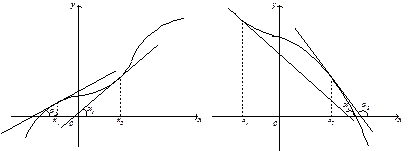
а б
Рис. 1. Зростаюча (а) та спадна функція (б)
Якщо дотичні до кривої на деякому проміжку спрямовані під гострими кутами до осі абсцис (рис. 1, а), то функція зростає, якщо під тупими (рис. 1, б), то спадає.
Приклад 1.1. Знайти інтервали монотонності функцій:
а) 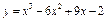 ; б)
; б) 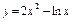 .
.
á а) Областю визначення цієї функції є множина 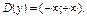
Знаходимо похідну функції: 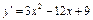 . Очевидно, що
. Очевидно, що 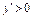 , якщо
, якщо 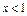 та
та 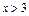 і
і  якщо
якщо  , тобто функція зростає на інтервалах
, тобто функція зростає на інтервалах 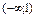 і
і 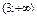 та спадає на інтервалі (1; 3) (рис. 2.)
та спадає на інтервалі (1; 3) (рис. 2.)

Рис. 2. Інтервали монотонності функції 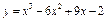
б) Функція 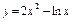 визначена на множині
визначена на множині 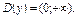
Визначаємо похідну:  .
.
Розв’язуючи нерівності 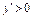 і
і  методом інтервалів, отримаємо, що ця функція зростає, якщо
методом інтервалів, отримаємо, що ця функція зростає, якщо 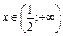 і спадає, якщо
і спадає, якщо 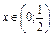 (рис. 3).
(рис. 3).

Рис. 3. Інтервали монотонності функції