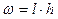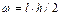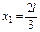Главная страница
Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
|
Определимых системах
Литература: [1] §5.4-5.6; [2] §104-107; [3] §38-40; [4] §VIII.3-VIII.4; [5] §6.1; [11] §5.6, 5.7; [12] §3.2.
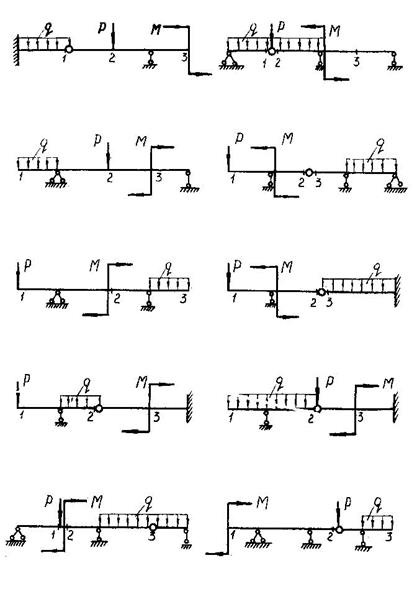
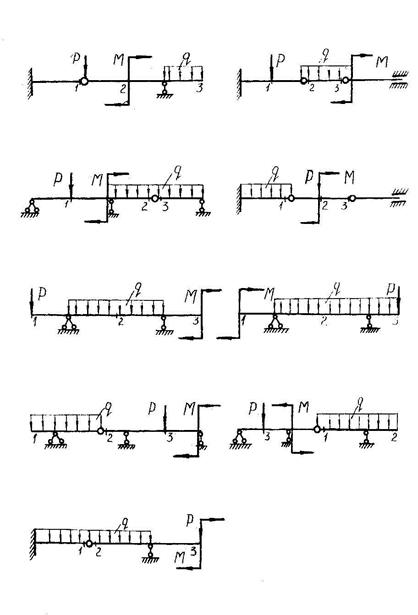
Задача 4.1 Для балок, схемы которых изображены на рис. 4.1, определить способом Верещагина вертикальное перемещение Δ или угол поворота φ одного из указанных сечений. Жесткость балки на изгиб EJ=4ּ 105 Н ּ м2. Остальные данные взять из табл. 4.1.
Таблица 4.1
| № строки
| Номер схемы
| P
кН
| q
кН/м
| М
кН ּ м
| l1
м
| l2
м
| l3
м
| Номер сечения
| Вид перемещения
| Вариант А

| Вариант В

| | 1
|
|
|
|
|
|
|
|
|
| φ
| | 2
|
|
|
|
|
|
|
|
|
| Δ
| | 3
|
|
|
|
|
|
|
|
|
| φ
| | 4
|
|
|
|
|
|
|
|
|
| Δ
| | 5
|
|
|
|
|
|
|
|
|
| φ
| | 6
|
|
|
|
|
|
|
|
|
| Δ
| | 7
|
|
|
|
|
|
|
|
|
| φ
| | 8
|
|
|
|
|
|
|
|
|
| Δ
| | 9
|
|
|
|
|
|
|
|
|
| φ
| | 0
|
|
|
|
|
|
|
|
|
| Δ
| |
| Е
| д
| е
| д
| е
| е
| д
| д
| е
|
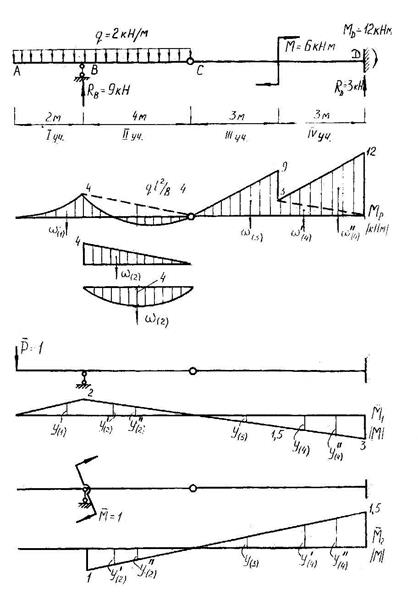
Пример выполнения задачи 4.1. Для балки, изображенной на
рис. 4.2, а, определить вертикальное перемещение сечения 1 и угол поворота сечения 2. Жесткость балки на изгиб постоянна и равна EJ= 5ּ 102 кН ּ м2. Остальные данные показаны на рисунке.
Решение. Определение перемещений от действия внешней нагрузки в стержневых системах, работающих на изгиб, проводится с помощью интеграла Мора
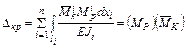 , (4.1) , (4.1)
который при постоянной на участках изгибной жесткости удобнее вычислять способом Верещагина
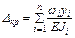 . (4.2) . (4.2)
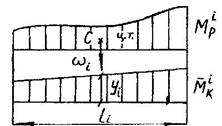
В формулах (4.1) и (4.2):  и и  – выражения изгибающих моментов в произвольном сечении i-го рассматриваемого участка от действия заданной внешней нагрузки и обобщенного усилия – выражения изгибающих моментов в произвольном сечении i-го рассматриваемого участка от действия заданной внешней нагрузки и обобщенного усилия 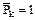 , приложенного в направлении искомого обобщенного перемещения Δ кр; ω i - площадь эпюры , приложенного в направлении искомого обобщенного перемещения Δ кр; ω i - площадь эпюры  и и  лежат по одну сторону оси стержня, то произведение ω iyi берется со знаком " +", а если они лежат по разные стороны. то произведение ω iyi принимает знак " –". лежат по одну сторону оси стержня, то произведение ω iyi берется со знаком " +", а если они лежат по разные стороны. то произведение ω iyi принимает знак " –".
Для определения вертикального перемещения сечения 1 необходимо построить эпюру  от действия внешней нагрузки (рис. 4.2, б) и эпюру от действия внешней нагрузки (рис. 4.2, б) и эпюру 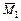 от действия силы от действия силы 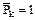 , приложенной вертикально в точке 1 (рис. 4.2, в). При определении угла поворота сечения в точке 2 строится эпюра , приложенной вертикально в точке 1 (рис. 4.2, в). При определении угла поворота сечения в точке 2 строится эпюра 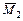 от действия единичного изгибающего момента от действия единичного изгибающего момента 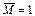 , приложенного в точке 2 (рис. 4.2, г). Построение указанных эпюр моментов проводим с помощью метода сечений, предварительно определяя реакции, возникающие в опорах (см. контрольную работу №1). При определении на участках площадей эпюры Мр и положения их центров тяжести воспользуемся табл. 4.2, в которой приведены наиболее часто встречающиеся случаи. Более сложные фигуры могут быть получены из приведенных путем их разбиения на простые. , приложенного в точке 2 (рис. 4.2, г). Построение указанных эпюр моментов проводим с помощью метода сечений, предварительно определяя реакции, возникающие в опорах (см. контрольную работу №1). При определении на участках площадей эпюры Мр и положения их центров тяжести воспользуемся табл. 4.2, в которой приведены наиболее часто встречающиеся случаи. Более сложные фигуры могут быть получены из приведенных путем их разбиения на простые.
Таблица 4.2
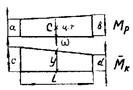
Число участков по построенным эпюрам равно четырем (их номера показаны на рис. 4.2, а). При этом на втором участке криволинейную фигуру эпюры Мр разобьем на треугольник и параболический сегмент (рис. 4.2, б) а на четвертом участке– трапецию на два треугольника. Найдем по участкам площади фигур эпюры Мр
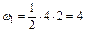 , ,  , ,  , ,
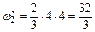 , ,  , , 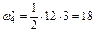
и соответствующие ординаты yi на эпюре 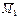 под их центрами тяжести под их центрами тяжести
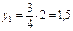 , , 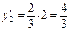 , ,  , , 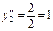 , ,
 , , 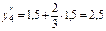 . .
Подставляя найденные значения площадей 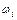 эпюры Мр и ординаты yi эпюры эпюры Мр и ординаты yi эпюры 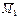 в формулу (4.2) и учитывая взаимное расположение указанных эпюр (или знаки произведений в формулу (4.2) и учитывая взаимное расположение указанных эпюр (или знаки произведений 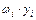 ), определим вертикальное перемещение точки 1 ), определим вертикальное перемещение точки 1
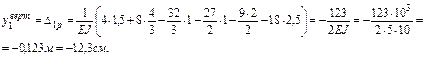
Следует отметить, что на 4-м участке произведение  может быть вычислено с помощью формулы " перемножения" трапеции (табл. 4.2, №5) может быть вычислено с помощью формулы " перемножения" трапеции (табл. 4.2, №5)
 . .
Найденное значение перемещений точки 1 имеет знак " –". Следовательно. точка 1 перемещается вверх, в сторону, противоположную действию единичной силы 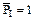 . .
Для определения угла поворота φ 2 сечения 2 вычислим ординаты yi на построенной от действия единичного момента 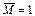 эпюре эпюре 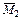 (рис. 4.2, г): (рис. 4.2, г):
 , , 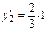 , ,  , , 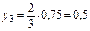 , ,
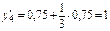 , , 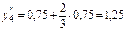 . .
и, используя выше найденные значения площадей ω i, фигур эпюры, Мр, по формуле (4.2) получаем
                                                   
                                                   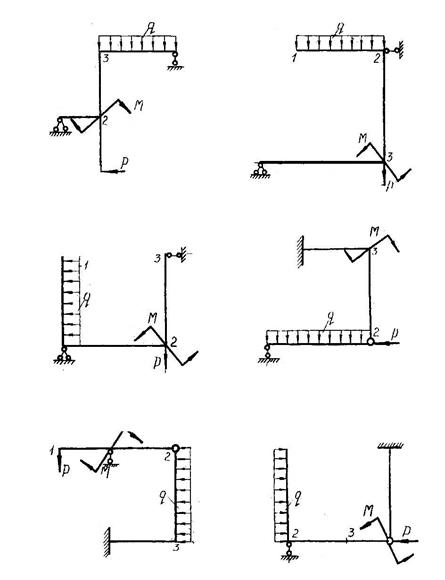
 
          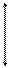                        
|





















































































































































































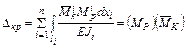 , (4.1)
, (4.1)
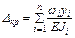 . (4.2)
. (4.2)  и
и  – выражения изгибающих моментов в произвольном сечении i-го рассматриваемого участка от действия заданной внешней нагрузки и обобщенного усилия
– выражения изгибающих моментов в произвольном сечении i-го рассматриваемого участка от действия заданной внешней нагрузки и обобщенного усилия 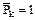 , приложенного в направлении искомого обобщенного перемещения Δ кр; ω i - площадь эпюры
, приложенного в направлении искомого обобщенного перемещения Δ кр; ω i - площадь эпюры  и
и  лежат по одну сторону оси стержня, то произведение ω iyi берется со знаком " +", а если они лежат по разные стороны. то произведение ω iyi принимает знак " –".
лежат по одну сторону оси стержня, то произведение ω iyi берется со знаком " +", а если они лежат по разные стороны. то произведение ω iyi принимает знак " –". от действия внешней нагрузки (рис. 4.2, б) и эпюру
от действия внешней нагрузки (рис. 4.2, б) и эпюру 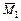 от действия силы
от действия силы 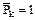 , приложенной вертикально в точке 1 (рис. 4.2, в). При определении угла поворота сечения в точке 2 строится эпюра
, приложенной вертикально в точке 1 (рис. 4.2, в). При определении угла поворота сечения в точке 2 строится эпюра 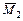 от действия единичного изгибающего момента
от действия единичного изгибающего момента 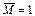 , приложенного в точке 2 (рис. 4.2, г). Построение указанных эпюр моментов проводим с помощью метода сечений, предварительно определяя реакции, возникающие в опорах (см. контрольную работу №1). При определении на участках площадей эпюры Мр и положения их центров тяжести воспользуемся табл. 4.2, в которой приведены наиболее часто встречающиеся случаи. Более сложные фигуры могут быть получены из приведенных путем их разбиения на простые.
, приложенного в точке 2 (рис. 4.2, г). Построение указанных эпюр моментов проводим с помощью метода сечений, предварительно определяя реакции, возникающие в опорах (см. контрольную работу №1). При определении на участках площадей эпюры Мр и положения их центров тяжести воспользуемся табл. 4.2, в которой приведены наиболее часто встречающиеся случаи. Более сложные фигуры могут быть получены из приведенных путем их разбиения на простые.





































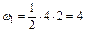 ,
,  ,
,  ,
,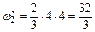 ,
,  ,
, 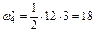
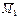 под их центрами тяжести
под их центрами тяжести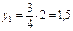 ,
, 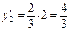 ,
,  ,
, 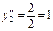 ,
, ,
, 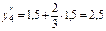 .
.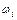 эпюры Мр и ординаты yi эпюры
эпюры Мр и ординаты yi эпюры 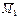 в формулу (4.2) и учитывая взаимное расположение указанных эпюр (или знаки произведений
в формулу (4.2) и учитывая взаимное расположение указанных эпюр (или знаки произведений 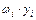 ), определим вертикальное перемещение точки 1
), определим вертикальное перемещение точки 1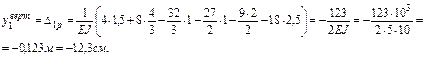
 может быть вычислено с помощью формулы " перемножения" трапеции (табл. 4.2, №5)
может быть вычислено с помощью формулы " перемножения" трапеции (табл. 4.2, №5) .
.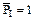 .
.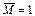 эпюре
эпюре 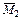 (рис. 4.2, г):
(рис. 4.2, г): ,
, 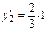 ,
,  ,
, 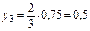 ,
,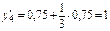 ,
, 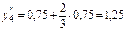 .
.