Пример выполнения задачи 8.1

Схема рамы, действующая нагрузка и основные геометрические размеры показаны на рис. 8.2, а. Отношение жесткостей стержней рамы 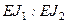=2, а внешних сил ; .

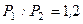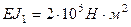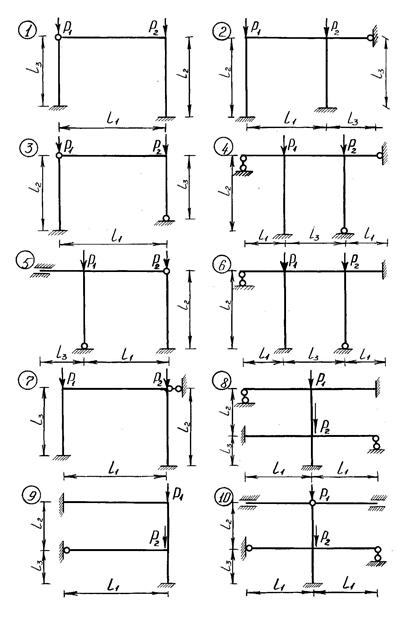
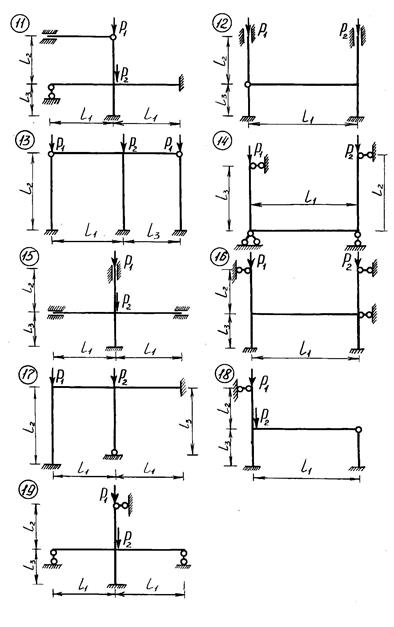
Решение. Рама дважды кинематически неопределима. Основная система метода перемещений (МП) показана на рис. 8.2, б. Определим параметры критической нагрузки V_i; для стержней, испытывающих сжатие (стержни 1 и 2 на рис. 8.2, б)

; ; .

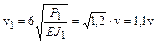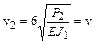Система канонических уравнений МП имеет вид:

r₁₁ Z₁+r₁₂ Z₂ = 0;

r₂₁ Z₁+r₂₂ Z₂= 0.(8.1)

Для нахождения коэффициентов r_ij (i, j=1, 2), входящих в (8.1), построим в основной системе с помощью таблицы 8.2 эпюры изгибающих моментов от единичных перемещений z_i=1 и рассмотрим равновесие узла А и верхней части рамы (рис. 8.2, д). Используя статический метод (см. контрольную работу №7), обычным путем вычислим коэффициенты r_ij системы (8.1)

.

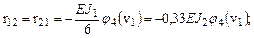
Система уравнений (8.1) имеет ненулевое решение (z_i≠ 0), если определить, составленный из коэффициентов r_ij, равен нулю, т.е.

. (8.2)

Раскрывая определитель и подставляя найденные значения коэффициентов r_ij в (8.2), приходим и следующему трансцендентному уравнению устойчивости

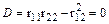(8.3)

или . (8.3)

решение которого находим методом последовательных приближений. Параметр v = v ₂ для второго стержня может изменяться в следующих пределах π /2 < v < π /0, 7. Нижний предел соответствует балке, защемленной с одной стороны и свободной с другой (μ =2), а верхний–защемленной с одной стороны и шарнирно опертой с другой стороны (μ =0, 7, рис. 8.2, е). Учитывая при этом, что стойки рамы находятся в условиях, близких к нижнему пределу, задаемся следующими значениями V:

1) v=v₂=2, 0; v₁=1, 1v=2, 19.

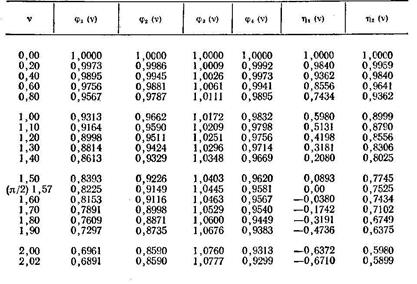
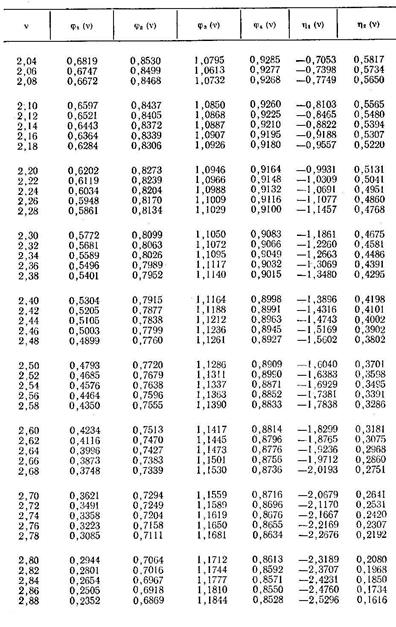
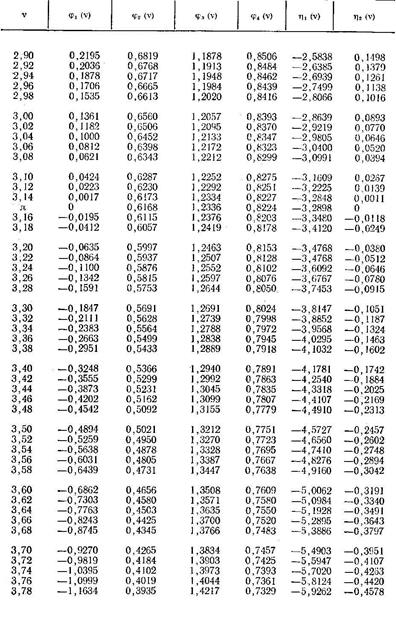
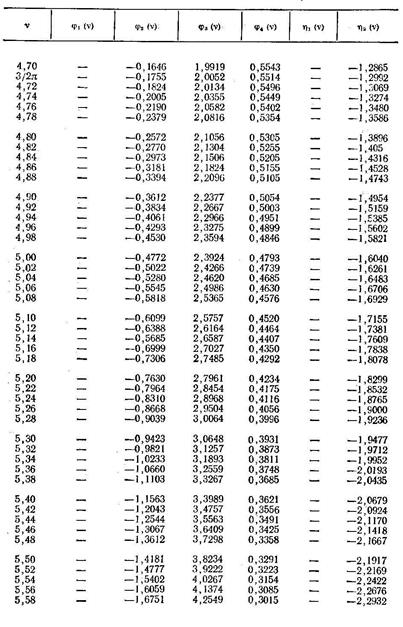
По таблице 8.4 последовательно находим:

φ ₂(v₁)=0, 8290; φ ₄(v₁)=0, 9172; η ₂(v₁)=0, 5176; η ₁(v₂)=-0, 6372.

Отсюда определяются значения коэффициентов r _ij и определителя D:

r₁₁=2, 853 EJ₂ r₁₂=-0, 3057 EJ₂; r₂₂=0, 0398 EJ₂; D=0, 02(EJ₂)²> 0.

2) v=v₂=2, 1; v₁=2, 31. Аналогично вычисляем:

φ ₂(v₁)=0, 8081; φ ₄(v₁)=0, 9075; η ₂(v₁)=0, 4628; η ₁(v₂)=-0, 8103;

r₁₁=2, 825 EJ₂; r₁₂=-0, 3025 EJ₂; r₂₂=0, 0289 EJ₂; D=0, 01(EJ₂)²< 0.

На интервале 2, 0< v< 2, 1 изменяется знак определителя D. Следовательно, в указанном интервале находится корень уравнения устойчивости (8.3). Принимая, что на интервале 2, 0< v< 2, 1 функция D изменяется по линейному закону, построим в масштабе график изменения определителя D в зависимости от параметра v (рис. 8.2, ж). Точка пересечения построенной прямой приближенно определяет корень решения уравнения (8.3): v=v₂=2, 07; v₁=2, 27.

Критическая нагрузка для рассматриваемой рамы:

.

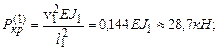
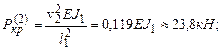
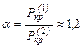Для нахождения формы потери устойчивости, соответствующей найденным значениям критических нагрузок, подставим значения коэффициентов r_ij в первое или второе уравнения системы канонических уравнений (8.1) МП ( φ ₂(v₁=2, 27)=0, 8152; φ ₄(v₁)=0, 9108; η ₂(v₁)=0, 4814; η ₁(v₂=2, 07)= – 0, 7573; r₁₁=2, 837EJ₂; r₁₂=-0, 3031EJ₂; r₂₂=0, 0324 EJ₂ ).

; .

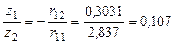z₁=0, 107z₂. Форма потери устойчивости рамы (z₂=1; z₁=0, 107) показана на рис. 8.2, з.

8.2. РАСЧЕТ РАМ И БАЛОК С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙСВОБОДЫ НА ДЕЙСТВИЕ ВИБРАЦИОННОЙ