
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример решения задачи 6
|
|
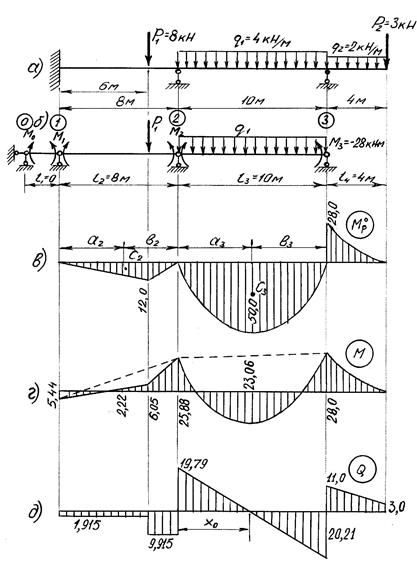
Для заданной на рис.6.2, а неразрезной балки выполнить расчеты согласно условию задачи 6.
Р ешение. Балка имеет пять опорных связей С0=5. Степень статической неопределимости
Построение эпюры М и Q от действия постоянной нагрузки. Для этого выберем основную систему, введя шарниры над опорами и превратив тем самым неразрезную балку в совокупность однопролетных шарнирно опертых балок. Положительные направления М показаны на рис. 6.2, б. Отбросив консоль, на правой опоре прикладываем момент 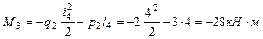 , а затем заделку слева заменяем дополнительным пролетом длиной l0=0. Пронумеруем опоры слева направо, начиная с нуля. Всем параметрам, относящимся к данному пролету, присвоим индекс по номеру правой опоры.
, а затем заделку слева заменяем дополнительным пролетом длиной l0=0. Пронумеруем опоры слева направо, начиная с нуля. Всем параметрам, относящимся к данному пролету, присвоим индекс по номеру правой опоры.
|

|
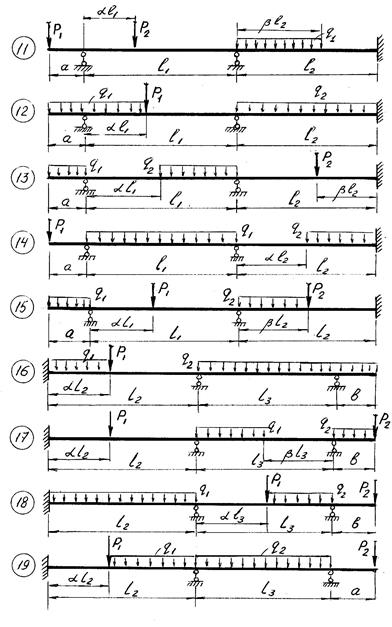
Таблица 6.1
| Номер строки | Номер схемы | L1 | l2 | l3 | а | в | p1 | p2 | q1 | q2 | α | β | |
| Вар. А д +е< 10 | Вар. В д +е> 10 | м | кН | кН/м | |||||||||
| 1 2 3 4 5 6 7 8 9 10 | 1 2 3 4 5 6 7 8 9 10 | 11 12 13 14 15 16 17 18 19 | 6 8 10 11 12 9 7 5 4 6 | 4 5 6 7 8 9 10 11 12 10 | 6 7 8 9 10 11 12 4 5 6 | 1, 5 2 3 1, 5 2 3 1, 5 2 3 1, 5 | 5 6 7 10 9 8 1 2 3 4 | 5 6 7 10 9 8 1 2 3 4 | 2 3 4 5 7 8 9 10 11 | 2 3 4 5 6 7 8 9 10 11 | 10 9 8 7 6 5 4 3 2 1 | 0, 25 0, 4 0, 5 0, 75 0, 5 0, 33 0, 4 0, 25 0, 5 0, 75 | 0, 75 0, 6 0, 25 0, 33 0, 5 0, 4 0, 25 0, 75 0, 4 0, 33 |
| е | е | д | е | г | е | д | д | е | д | е | д | е |
Загрузив основную систему заданной нагрузкой, определяем реакции опор соответствующих однопролетных балок и строки эпюры изгибающих моментов для каждой балки в отдельности (рис. 6.2, в).
Уравнение трех моментов для i-й опоры имеет вид (см.2.1[7])
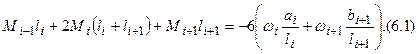 . (6.1)
. (6.1)
Здесь Мi-1, Mi, Mi+1 – моменты соответственно над i-1, i, i+1 опорами;
li, li+1 – длины i и i+1 пролетов;
ω i, ω i+1 - площади эпюр изгибающих моментов от заданной нагрузки в основной системе;
аi, bi+1 – расстояния от центров тяжести площадей ω i и ω i+1 соответственно до левой опоры i пролета и до правой опоры i+1 пролета.
Составим уравнения трех моментов для опор 1 и 2:
|
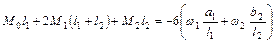
(6.2)
 .
.
В рассматриваемой задаче М0=0, l1=0, М3=-28кНּ м, ω 2=1/2ּ 12ּ 8=48кНּ м2, 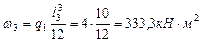 ,
, 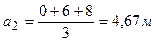 ,
, 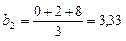 ,
, 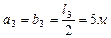 .
.
Подставим найденные значения в уравнения (6.2)
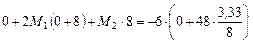 ;
;
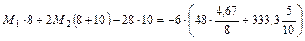 .
.
Решая полученную систему уравнений, находим: М1=5, 44 кНּ м, М2=-25, 88 кНּ м. По этим значениям построим эпюру опорных моментов М0, которая показана на рис. 6.2, г пунктирной линией.
Окончательную эпюру М построим, суммируя эпюры М 0p и М0.
Для неразрезных балок эпюры М и Q могут быть построены также и по следующим формулам:
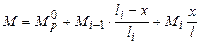 ;
;
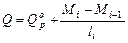 , (6.3)
, (6.3)
где 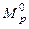 и
и 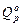 – значения М и Q от заданной нагрузки для простых шарнирно опертых балок основной системы.
– значения М и Q от заданной нагрузки для простых шарнирно опертых балок основной системы.
Используя первую формулу (6.3), определим ординаты эпюры М в характерных сечениях:
в середине второго пролета
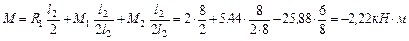 ;
;
в сечении где приложена сила Р1
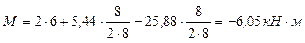 ;
;
в середине третьего пролета
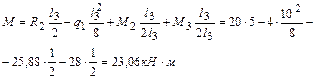 .
.
Эпюра М показана на рис.6.2, г.
Вычислим значения поперечной силы Q в характерных сечениях:
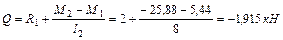 ,
,
на втором участке второго пролета
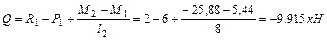 .
.
На третьем участке поперечная сила изменяется согласно уравнению
 (6.4)
(6.4)
в начале третьего участка 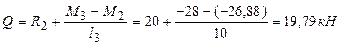 ; в конце третьего участка
; в конце третьего участка 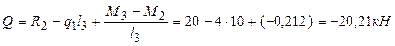 .
.
Эпюра Q показана на рис.6.2, д. Абсцисса x0 сечения, где Q=0, определяется из (6.4)
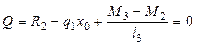 . Отсюда x0 =4, 95 м.
. Отсюда x0 =4, 95 м.
Тогда 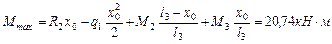 .
.
Построение эпюры изгибающих моментов от временной нагрузки Интенсивность временной нагрузки равна
. 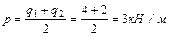 .
.
Для построения эпюры изгибающих моментов применим метод моментных фокусных отношений. Предварительно определим левые и правые фокусные отношения (см. 2.2 [7)
левые: К2=2; 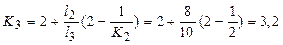 ;
;
правые: 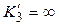 ;
; 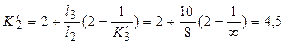 .
.
Зная моментные фокусные отношения и моменты над опорами загруженного i-го пролета, определяем моменты над остальными опорами справа и слева соответственно по формулам
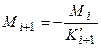 ,
, 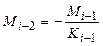 . (6.5)
. (6.5)
При загружении только i -го пролета моменты над его опорами определяем по формулам (см. формулу 2.8 [7]): (6.6)
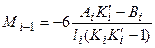 ,
, 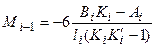 , (6.6)
, (6.6)
где 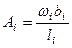 ,
, 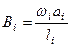 . (6.7)
. (6.7)
От нагрузки, находящейся во втором пролете, определяем величины А2 и В2 по формулам (6.7):
 ,
,
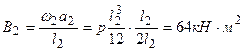 .
.
По формулам (6.6) вычислим моменты для левой и правой опоры загруженного пролета:
 ,
,
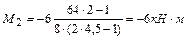 .
.
Момент над третьей опорой найдем, используя формулу (6.5)
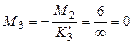 .
.
Эпюра изгибающих моментов показана на рис. 6.3, в.
Нагрузка находится в третьем пролете.
По формулам (6.7) находим
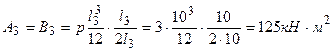 .
.
Вычислим моменты над левой и правой опорами загруженного пролета:
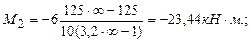
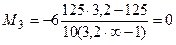 .
.
Момент над третьей опорой (в заделке) определяем по (6.5)
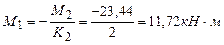 .
.
Эпюра изгибающих моментов показана на рис. 6.3, д.
Нагрузка приложена на консоли. При этом момент на третьей опоре будет равен
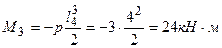 .
.
Моменты слева над второй и первой опорами найдем, используя (6.5):
|
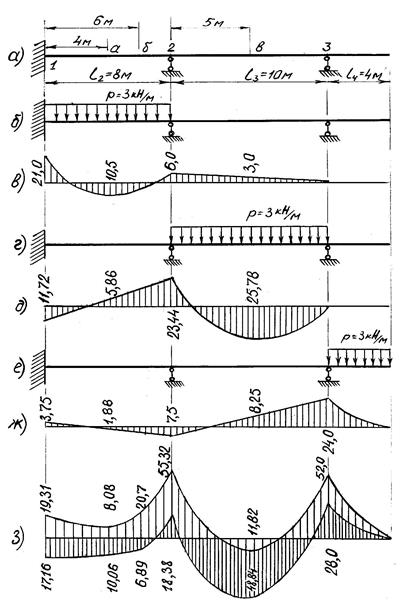
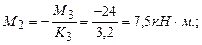 ,
, 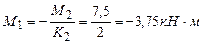 .
.
Эпюра изгибающих моментов показана на рис. 6.3, ж.
Построение огибающей эпюры моментов. Для определения максимального момента Mmax в данном сечении к моменту от постоянной нагрузки в этом сечении. Аналогично для определения минимального момента Mmin в данном сечении к моменту от постоянной нагрузки прибавим все отрицательные моменты от временной нагрузки; т.е.
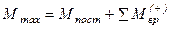 ,
, 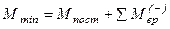 .
.
Для построения огибающей эпюры моментов определим ординаты Mmax и Mmin в характерных сечениях балки, обозначенных на рис. 6.2, а цифрами и буквами 1, а, б, 2, в, 3.
Результаты вычислений сведены в табл. 6.2.
Таблица 6.2
| Сечение | М пост КНּ м | М от временной нагрузки | Mmax кНּ м | Mmin кНּ м | ||
| нагрузка в 1 пролете | нагрузка во 2 пролете | нагрузка в 3 пролете | ||||
| 5, 44 | -21, 00 | 11, 72 | -3, 75 | 17, 16 | -19, 31 | |
| а | -2, 22 | 10, 50 | -5, 86 | 1, 88 | 10, 16 | -8, 08 |
| б | -6, 05 | 8, 25 | -14, 65 | 4, 69 | 6, 89 | -20, 70 |
| -25, 88 | -6, 00 | -23, 44 | 7, 50 | -18, 38 | -55, 32 | |
| в | 23, 06 | -3, 00 | 25, 78 | 8, 25 | 48, 84 | 11, 81 |
| -28, 00 | 0, 00 | 0, 00 | -24, 00 | -28, 00 | -52, 00 |
Огибающая эпюра изгибающих моментов представлена на рис. 6.3, э
Контрольная работа №7