
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Чертеж точки
|
|
Прямоугольные проекции точки на плоскостях проекций получатся как основания перпендикуляров, опущенных из данной точки на каждую из плоскостей проекций.
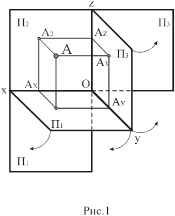
На рис.1 представлено наглядное изображение трех взаимно-перпендикулярных плоскостей. Линии пересечения этих плоскостей – x, y, z -- сходятся в одной точке 0 (координатные оси и начало координат). Чтобы получить плоский чертеж, повернем плоскость П1 вокруг оси Х до совмещения с плоскостью П2, а плоскость П3 -- вокруг оси Z до совмещения с плоскостью П2.
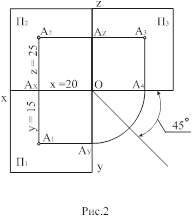
На рис. 2 представлен чертеж точки на три плоскости проекции. Точка А задана координатами: первая координата -- Х (абсцисса), вторая -- Y (ордината), третья -- Z (аппликата).
Построив проекции двух точек и соединив их, получим чертеж отрезка прямой. Чертеж трех точек может рассматриваться как отсек плоскости (плоскость в пространстве безгранична – мы ее ограничиваем отсеком).
Отрезок прямой может занимать различное положение в пространстве относительно плоскостей проекций:
а) быть параллельным одной плоскости проекций, и в этом случае он проецируется на эту плоскость проекций в натуральную величину (фронталь, горизонталь, профильная прямая).
б) параллелен двум плоскостям проекций (натуральная величина) и перпендикулярен к третьей плоскости проекции (горизонтально-проецирующая прямая, фронтально-проецирующая прямая и профильно-проецирующая прямая);
в) не параллелен и не перпендикулярен ни одной из плоскостей проекций – называется прямой общего положения. Проекции этого отрезка на чертеже по величине меньше отрезка. Имея на чертеже две проекции отрезка, можно определить по ним натуральную величину и углы наклона к плоскостям проекций.
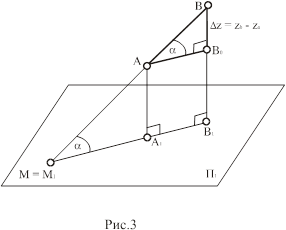
Теорема: гипотенуза прямоугольного треугольника является натуральной величиной прямой, один катет которого – проекция на эту плоскость проекций, а второй – разность расстояний концов отрезка от данной плоскости проекций. Угол между катетом – проекцией и гипотенузой является углом наклона прямой к данной плоскости проекции.
Как показано на рис. 3 АВ является гипотенузой прямоугольного треугольника АВВ0, у которого один катет АВ0=А1В1 (т.е. проекция на плоскость П1), а второй ВВ0=ZB - ZA.
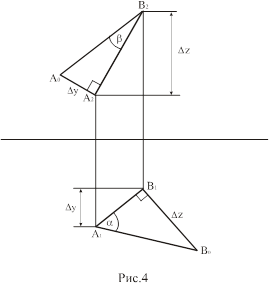
На рис. 4 определены натуральная величина и углы наклона к плоскостям проекций П1 и П2.
Для решения задачи 1 контрольной работы необходимо знать теорему о проекциях плоских углов, которая звучит так: любой по величине угол образованный пересекающимися или скрещивающимися прямыми, проецируется в натуральную величину на ту плоскость проекций, которой параллельны обе его стороны (рис.5).
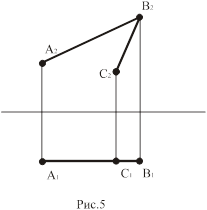
Прямой угол проецируется в натуральную величину и тогда, когда только одна из его сторон параллельна плоскости проекций.
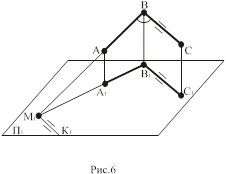
Пусть имеется прямой угол АВС (рис.6), в котором ВС║ П1, а сторона АВ не параллельна П1. Докажем, что Ð А1В1С1=Ð АВС=90°. Продолжим сторону АВ до пересечения со своей проекцией А1В1 в точке М1, через точку М1 проведем прямую М1К1║ В1С1, прямая М1К1 будет параллельна и ВС, угол ВМ1К1 является прямым. Согласно обратной теореме о трех перпендикулярах угол ВМ1К1 также прямой, следовательно, угол А1В1С1 – прямой.

На рис.7 представлен чертеж, где Вс является горизонталью, из точки А восстановили перпендикуляр к ВС (угол А1В1С1 – прямой).
При решении задачи 1 необходимо построить две проекции отсека плоскости АВС, провести в плоскости главные линии – горизонталь и фронталь, из точки D восстановить перпендикуляр к главным линиям, найти точку встречи этого перпендикуляра с плоскостью АВС.
Чтобы определить точку встречи прямой с плоскостью необходимо заключить данную прямую в плоскость (проецирующую) и построить линию пересечения двух плоскостей.
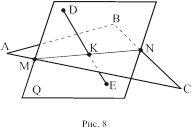
Прямая DE пересекает плоскость АВС (рис. 8), DE заключается в плоскость Q, определяется линия пересечения плоскости Q и АВС - это MN. Рассматривая взаимное расположение прямых DE и MN определяем точку К, которая является точкой пересечения прямой DE и плоскости АВС (принадлежит прямой DE и плоскости АВС).
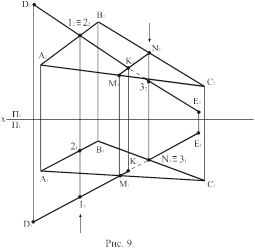
На рис.9 представлен чертеж этой же задачи. Плоскость Q является горизонтально-проецирующей, видимость прямой на фронтальной плоскости проекций определена с помощью фронтально конкурирующих точек 1 и 2. Положение точек на горизонтальной проекции - 1Ì DE, 2Ì АВ, точка 1 расположена ближе точки 2, следовательно, отрезок прямой DK на фронтальной проекции будет видимым. Чтобы определить видимость относительно горизонтальной плоскости проекций, нужно выбрать две конкурирующие точки (N и 3), точка N выше точки 3 (т.е. координата точки N больше координаты точки 3), значит, В1С1 будет видимая, а К1N1 - невидимая часть прямой.