
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Контрольная работа № 1. Данные для решения задачи берутся согласно варианту по таблице 1.
|
|
Данные для решения задачи берутся согласно варианту по таблице 1.
Таблица 1
| № вар. | Значения координат, мм | ||||||||||||||
| А | В | С | D | E | |||||||||||
| X | Y | Z | X | Y | Z | X | Y | Z | X | Y | Z | X | Y | Z | |
| 1. | |||||||||||||||
| 2. | |||||||||||||||
| 3. | |||||||||||||||
| 4. | |||||||||||||||
| 5. | |||||||||||||||
| 6. | |||||||||||||||
| 7. | |||||||||||||||
| 8. | |||||||||||||||
| 9. | |||||||||||||||
| 10. | |||||||||||||||
| 11. | |||||||||||||||
| 12. | |||||||||||||||
| 13. | |||||||||||||||
| 14. | |||||||||||||||
| 15. | |||||||||||||||
| 16. | |||||||||||||||
| 17. | |||||||||||||||
| 18. | |||||||||||||||
| 19. | |||||||||||||||
| 20. | |||||||||||||||
| 21. | |||||||||||||||
| 22. | |||||||||||||||
| 23. | |||||||||||||||
| 24. | |||||||||||||||
| 25. | |||||||||||||||
| 26. | |||||||||||||||
| 27. | |||||||||||||||
| 28. | |||||||||||||||
| 29. | |||||||||||||||
| 30. | |||||||||||||||
| 31. | |||||||||||||||
| 32. | |||||||||||||||
| 33. | |||||||||||||||
| 34. | |||||||||||||||
| 35. | |||||||||||||||
| 36. |

Задачи 1, 2





Рис. 10. а
Задача 3
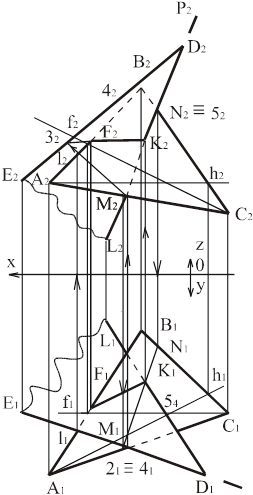
Рис. 10. б
Задача 1
Определить расстояние от точки D до плоскости АВС (пример на рис. 10. а).
Указания к задаче 1
Задачу выполняют в следующей последовательности:
1. по координатам своего варианта строят две проекции треугольника и точку D;
2. из точки D следует опустить перпендикуляр к плоскости, используя горизонталь и фронталь принадлежащие плоскости, при этом D1 ^ h1, D2 ^ f2;
3. перпендикуляр заключают во вспомогательную плоскость P2 (фронтально-проецирующую), которая пересекает АВС по линии MN;
4. на горизонтальной проекции определяем точку встречи (К1) перпендикуляра с плоскостью АВС, как результат пересечения M1N1 и перпендикуляра из проекции точки D1;
5. определяем натуральную величину (H.B.) расстояния от точки D до АВС методом прямоугольного треугольника. Гипотенуза прямоугольного треугольника является натуральной величиной прямой, один катет которого – проекция на данную плоскость проекций, а второй - разность расстояний концов отрезка от данной плоскости проекций (DZ). K1D0 является расстоянием от точки до плоскости.
Алгоритм решения задачи 1
1. A212 ê ê OX®h2
12 Ì B2C2®11Ì B1C1=h1
2. C121 ê ê OX®f1
21Ì A1B1®22 Ì A2B2=f2
3. D2 ^ f2; D1 ^ h1
D2 Ì P2; P2 Ç A2B2C2=M2N2
4. M1N1 Ç D1=K1; K2 Ì M2N2
5. D1K1 ^ D1D0 =DZ (ZD – ZK)
ç K1D0ç
Задача 2
Построить плоскость, параллельную заданной и отстоящую от нее на 30 мм (пример на рис. 10.а).
Указания к задаче 2
Задача решается аналогично первой:
1. Из любой точки, лежащей в плоскости, восстанавливают перпендикуляр (A2 ^ f2; А1 ^ h1);
2. на этом перпендикуляре выбирают произвольную точку F и определяют методом прямоугольного треугольника натуральную величину отрезка AF;
3. на натуральной величине определяют точку отстоящую от плоскости АВС на расстоянии 30 мм и возвращаются на проекции перпендикуляра (Е);
4. в точке Е строят, искомую плоскость, соблюдая условия параллельности плоскостей: если две плоскости параллельны, то две пересекающиеся прямые одной плоскости, параллельным двум пересекающимся прямым другой плоскости.
Алгоритм решения задачи 2
1. A212 ï ï OX®h2; 12 Ì B2C2®11 Ì B1C1=h1.
2. A1 ^ h1; A2 ^ f2; F2 и F1 – проекции произвольно взятой точки.
3. A2 ^ A2A0=DY(YA-YF); |A0F2|,
A0E0=30 мм; E0®E2®E1.
Задача 3
Через прямую DE провести плоскость ^ABC. Построить линию пересечения плоскостей, обозначив видимость (пример на рис. 10. б).