Випадкові процеси. Основні означення

Основні означення та імовірнісні характеристики стохастичних моделей

Випадкові процеси, як моделі сигналів в об’єктах технічної природи. Основні

означення випадкових процесів. Класифікація випадкових процесів. Стаціонарні випадкові процеси. Ергодичні процеси. Основні імовірнісні характеристики випадкових процесів. Числові характеристики випадкових процесів. Поняття про математичне сподівання и дисперсію. Функціональні характеристики випадкових процесів. Поняття про коваріаційну та

кореляційну функції, спектральну щільність потужності, функцію розподілу, щільність розподілу та характеристичну розподілу ймовірностей

Випадкові процеси, як моделі сигналів в об’єктах

Технічної природи

Адекватність моделі і явища. Формалізований підхід до задач теорії вимірювань та обробки сигналів пов’язаний із створенням та вивченням математичних моделей сигналів і шумів. Ці моделі потім повинні проходити перевірку з метою визначення їх придатності для опису реального фізичного явища або пристрою. Ніяка математична модель не може бути абсолютно адекватною реальному фізичному явищу і завжди повинна розглядатися як деяке більш або менш його вдале наближення. Однак в статистичній радіофізиці, теорії вимірювань, для спрощення слово ’’модель’’ часто випускається. Наприклад, замість ’’модель амплітудно модульованого сигналу’’ просто говорять ’’сигнал, модульований по амплітуді’’.

Моделі, які враховують лише фізичну суть явища, що відбувається, і не обов'язково враховують кількісні співвідношення, звуться фізичними моделями (ФМ). В техніці під ФМ, як правило, розуміють зменшену копію реального об’єкту. Наприклад, в якості моделі потужного електричного генератору теплових електростанцій, можна використовувати звичайний малопотужний електричний двигун. Це зумовлено тим, що фізичні процеси, які супроводжують роботу різних за габаритами електричних машин підкоряються однаковим фізичним законам і, істотно, описуються однаковими аналітичними співвідношеннями.

Моделі, які будуються, виходячи з деякої початкової системи аксіом шляхом логічних викладок, називають аксіоматичними, а моделі, які будуються, виходячи з конструкції реального або ідеалізованого процесу чи явища, називають конструктивними. Конструктивні моделі зустрічаються частіше в прикладних, а аксіоматичні - в теоретичних дослідженнях.

Випадкові процеси. Основні означення

ОЗНАЧЕННЯ 3.1. Параметричне сімейство (сукупність) дійсних випадкових величин називається дійсним випадковим процесом.

Дійсний випадковий процес позначається як параметрична множина 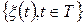, де 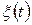- символ елементів множини, 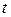- параметр, - область визначення, що являє собою інтервал (неперервна область), або множину ізольованих точок (дискретна множина), або те і інше одночасно. Самі випадкові величини 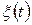, що утворюють сукупність, можуть в свою чергу бути неперервними, дискретними або загального виду.

ОЗНАЧЕННЯ 3.2. Крива, яка з'являється внаслідок одного спостереження над випадковим процесом, називається його реалізацією або вибірковою функцією і позначається як .

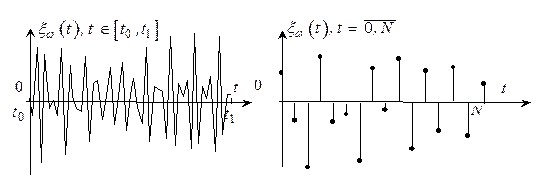
а) б)

Рис. 3.1

На рис. 3.1. наведено графічне зображення а) - неперервної реалізації, б) - дискретної реалізації, які мають місце на практиці.

ОЗНАЧЕННЯ 3.3. Сімейство функцій

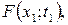
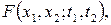
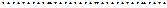(3.1)

,

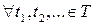називається послідовністю скінченновимірних функцій розподілів процесу 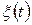, коли вона задовольняє таким умовам.

1. Інваріантності відносно перестановки індексів при 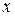та 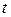одночасно (умова симетрії):

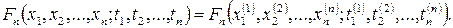
Тут 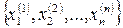- довільна перестановка елементів множини і аналогічно для .

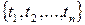2. Узгодженості:

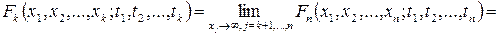
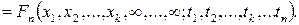
Випадковий процес вважається повністю заданим, якщо задана послідовність його скінченновимірних функцій розподілу для всіх моментів часу 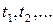, або відповідна послідовність характеристичних функцій. Не всякий випадковий процес можна задати за допомогою послідовності (3.1). Процеси, які повністю задаються послідовністю (3.1) називаються сепарабельними. Основні означення і властивості, що стосуються функції розподілу 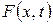, наведено у підрозділі 3.6 даної лекції.

ОЗНАЧЕННЯ 3.4. Процес 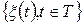називається комплекснозначним, коли його дійсна та уявна частини суть дійсні випадкові процеси, тобто коли його можна подати у вигляді

,

де і визначаються згідно з означенням 1 і задаються на одному й тому ж ймовірнісному просторі.

ОЗНАЧЕННЯ 3.5. Комплекснозначний випадковий процес 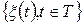називається гільбертовим, коли 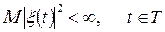, де М - оператор математичного сподівання випадкового процесу .

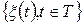Іншими словами, дійсний гільбертів процес в довільний момент часу має скінченну потужність, що є необхідною умовою його фізичної реалізовності.