
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Стаціонарні випадкові процеси
|
|
Фізичний процес можна описати у будь-який момент часу шляхом осереднення за множиною вибіркових функцій, що характеризують досліджуваний процес. Розглянемо, наприклад, множину вибіркових функцій (так званий ансамбль), що утворюють випадковий процес (рис. 3.3)
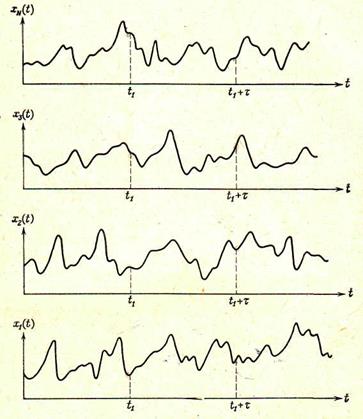
|
Рис. 3.3.
Середнє значення (перший момент розподілу) випадкового процесу 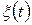 в момент часу
в момент часу 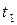 може бути знайдено шляхом підсумовування миттєвих значень кожної вибіркової функції ансамблю в момент
може бути знайдено шляхом підсумовування миттєвих значень кожної вибіркової функції ансамблю в момент 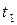 і ділення цієї суми на число вибіркових функцій. Аналогічним чином кореляція між значеннями випадкового процесу
і ділення цієї суми на число вибіркових функцій. Аналогічним чином кореляція між значеннями випадкового процесу 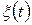 у два різних моменти (мішаний момент, що називається автокореляційною функцією, основні означення і властивості якої наведено у підрозділі 3.6 даної лекції) визначається шляхом осереднення за ансамблем добутків миттєвих значень цього процесу у моменти
у два різних моменти (мішаний момент, що називається автокореляційною функцією, основні означення і властивості якої наведено у підрозділі 3.6 даної лекції) визначається шляхом осереднення за ансамблем добутків миттєвих значень цього процесу у моменти 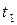 та
та 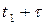 . Інакше кажучи, середнє значення
. Інакше кажучи, середнє значення 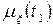 і автокореляційна функція
і автокореляційна функція  випадкового процесу
випадкового процесу 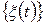 (фігурні дужки означають ансамбль вибіркових функцій) визначаються із співвідношень
(фігурні дужки означають ансамбль вибіркових функцій) визначаються із співвідношень
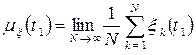 , (3.2)
, (3.2)
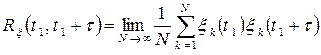 , (3.3)
, (3.3)
де 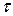 - час зсуву точки спостереження. При підсумовуванні передбачається, що поява всіх вибіркових функцій є рівноймовірною.
- час зсуву точки спостереження. При підсумовуванні передбачається, що поява всіх вибіркових функцій є рівноймовірною.
У тому випадку, коли функції 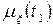 і
і  , що визначаються співвідношеннями (3.2) і (3.3), змінюються із зміною моменту часу
, що визначаються співвідношеннями (3.2) і (3.3), змінюються із зміною моменту часу 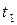 , випадковий процес
, випадковий процес 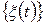 називається нестаціонарним. У окремому випадку, коли функції
називається нестаціонарним. У окремому випадку, коли функції 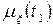 та
та  , є незалежними, випадковий процес
, є незалежними, випадковий процес 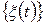 має назву слабо стаціонарного, або стаціонарного у широкому сенсі. Середнє значення слабо стаціонарних процесів постійне, а автокореляційна функція залежить тільки від величини зсуву
має назву слабо стаціонарного, або стаціонарного у широкому сенсі. Середнє значення слабо стаціонарних процесів постійне, а автокореляційна функція залежить тільки від величини зсуву 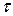 , тобто
, тобто 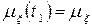 та
та 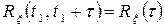 .
.
Для випадкового процесу 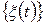 можна розрахувати нескінчену множину початкових і мішаних моментів більш високих порядків; їх сукупність повністю описує щільність розподілу досліджуваного процесу. Коли всі початкові і мішані моменти розподілу не залежать від часу, випадковий процес
можна розрахувати нескінчену множину початкових і мішаних моментів більш високих порядків; їх сукупність повністю описує щільність розподілу досліджуваного процесу. Коли всі початкові і мішані моменти розподілу не залежать від часу, випадковий процес 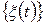 називається строго стаціонарним, або стаціонарним у вузькому сенсі.
називається строго стаціонарним, або стаціонарним у вузькому сенсі.
Слід зазначити, що будь-яка ймовірнісна задача вважається повністю вирішеною, якщо знайдено її щільність розподілу, або всі початкові і мішані моменти. Крім того, для багатьох практичних задач, що стосуються побудови і дослідження ймовірнісних моделей, доведення слабкої стаціонарності цілком досить для слушності припущенності про строгу стаціонарність процесу, що розглядається.