
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Характеристичну розподілу ймовірностей
|
|
До функціональних характеристик випадкових процесів відносяться наступні:
Коваріаційна та кореляційна функції випадкових процесів характеризують загальну залежність значень процесу у деякий певний момент часу від його значень в інший.
ОЗНАЧЕННЯ 3.6. Коваріацією (або автоковаріацією) гільбертового випадкового процесу 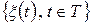 називається функція
називається функція
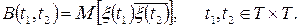 (3.8)
(3.8)
Зауважимо, що коваріація співпадає зі скалярним добутком випадкових величин 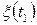 i
i 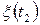 тобто
тобто
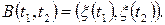
Якщо випадковий процес є дійсним, то формула (3.8) набуває вигляду

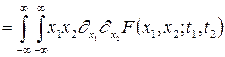 . (3.9)
. (3.9)
ОЗНАЧЕННЯ 3.7. Кореляційною (або автокореляційною) функцією гільбертового випадкового процесу 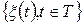 називається функція
називається функція
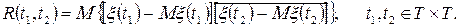 (3.10)
(3.10)
Між кореляційною та коваріаційною функціями має місце наступний зв'язок:
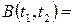
 (3.11)
(3.11)
Зауважимо, що для дійсного випадкового процесу 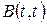 являє собою середню повну миттєву потужність,
являє собою середню повну миттєву потужність, 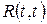 - середня миттєва потужність флуктуацій, а
- середня миттєва потужність флуктуацій, а 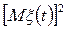 - середня миттєва потужність детермінованої складової, які віднесені до моменту часу
- середня миттєва потужність детермінованої складової, які віднесені до моменту часу 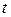 . Коли деякий дійсний випадковий процес
. Коли деякий дійсний випадковий процес 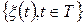 зазнає перетворення, закон якого задається динамічною характеристикою у вигляді функції
зазнає перетворення, закон якого задається динамічною характеристикою у вигляді функції  , то для вихідного процесу
, то для вихідного процесу  коваріація визначається таким чином:
коваріація визначається таким чином:
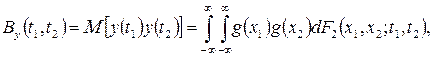
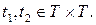 (3.12)
(3.12)
ОЗНАЧЕННЯ 3.8. Взаємною коваріаційною функцією двох гільбертових випадкових процесів 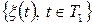 i
i  називається функція
називається функція
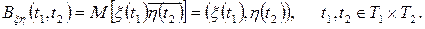 (3.13)
(3.13)
Аналогічно визначається і взаємна кореляційна функція двох процесів.
ОЗНАЧЕННЯ 3.9. Взаємною кореляційною функцією двох гільбертових випадкових процесів 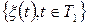 i
i  називається функція
називається функція
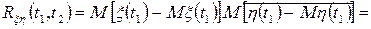
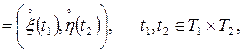 (3.14)
(3.14)
де 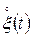 і
і 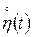 центровані гільбертові випадкові процеси:
центровані гільбертові випадкові процеси: 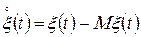 ,
,  .
.
Кореляційна функція фізичного процесу застосовується насамперед для дослідження залежності значень процесу в даний момент часу від певних значень цього процесу у минулому. Кореляційна функція гармонійного коливання або будь-якого іншого детермінованого процесу, власно кажучи, відмінна від нуля при всіх значеннях аргументу, тоді як кореляційна функція випадкового процесу при великих значеннях зсуву прямує до нуля (якщо 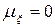 ). Тому, вочевидь, що кореляційна функція являє собою потужний засіб для виявлення детермінованих процесів, які можуть маскуватись випадковим фоновим шумом. Існують інші, менш наочні приклади використання кореляційної функції, але їх краще пояснити шляхом використання перетворення Фур’є цієї функції, яке носить назву спектральної щільності потужності.
). Тому, вочевидь, що кореляційна функція являє собою потужний засіб для виявлення детермінованих процесів, які можуть маскуватись випадковим фоновим шумом. Існують інші, менш наочні приклади використання кореляційної функції, але їх краще пояснити шляхом використання перетворення Фур’є цієї функції, яке носить назву спектральної щільності потужності.
Спектральна щільність потужності випадкового процесу описує загальну частотну структуру цього процесу через спектральну щільність середнього значення квадрату його значень. Середнє значення квадрату значень реалізації в інтервалі частот від  до
до  можна одержати, подаючи цю реалізацію на вхід смугового фільтру з вузькою смугою шляхом перепускання і осереднення піднесеної до квадрату функції (реалізації) на виході фільтру. Це осереднене значення квадрату наближається до точного його значення при прямуванні часу
можна одержати, подаючи цю реалізацію на вхід смугового фільтру з вузькою смугою шляхом перепускання і осереднення піднесеної до квадрату функції (реалізації) на виході фільтру. Це осереднене значення квадрату наближається до точного його значення при прямуванні часу  до нескінченності
до нескінченності
 . (3.15)
. (3.15)
В останньому співвідношенні 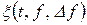 - складові функції
- складові функції 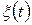 , яка має частоти в інтервалі від
, яка має частоти в інтервалі від  до
до  . При малих
. При малих  спектральну щільність можна визначити за допомогою наближеної рівності
спектральну щільність можна визначити за допомогою наближеної рівності
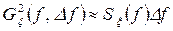 . (3.16)
. (3.16)
На основі останнього співвідношення можна сформулювати наступне означення.
ОЗНАЧЕННЯ 3.10. Спектральною щільністю потужності випадкового процесу  є функція, яка визначається наступним співвідношенням
є функція, яка визначається наступним співвідношенням
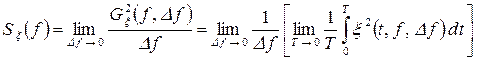 . (3.17)
. (3.17)
Слід зазначити, що величина 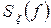 - завжди дійсна, невід’ємна функція.
- завжди дійсна, невід’ємна функція.
Важлива властивість спектральної щільності потужності полягає у її зв’язку з автокореляційною функцією. Зокрема, для стаціонарного процесу ці функції зв’язані перетворенням Фур’є
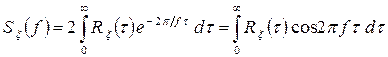 . (3.18)
. (3.18)
Перехід до останнього виразу можливий тому, що 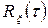 є парною функцією аргументу
є парною функцією аргументу 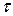 .
.
Середнє значення функції 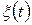 визначається спектральною щільністю потужності у відповідністю з співвідношенням
визначається спектральною щільністю потужності у відповідністю з співвідношенням
 ,
,
де 0- та 0+ означають, що нижня межа інтегрування береться зліва, а верхня – справа. Інакше, середнє значення функції 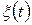 входить у функцію
входить у функцію 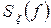 через дельта – функцію Дірака при нульовій частоті.
через дельта – функцію Дірака при нульовій частоті.
Повні ймовірнісні характеристики досліджуваного випадкового процесу 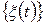 визначаються його щільністю розподілу ймовірностей або функцією розподілу. Розглянемо ці характеристики.
визначаються його щільністю розподілу ймовірностей або функцією розподілу. Розглянемо ці характеристики.
Щільність та функція розподілу ймовірностей надають можливість одержати повне вирішення будь-якої ймовірнісної задачі.
Щільність розподілу ймовірностей випадкового процесу 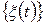 визначає ймовірність того, що значення процесу у довільний момент часу будуть знаходитись у певному інтервалі. На рис. 3.4 наведено деяку реалізацію
визначає ймовірність того, що значення процесу у довільний момент часу будуть знаходитись у певному інтервалі. На рис. 3.4 наведено деяку реалізацію 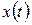 як функцію часу. Ймовірність того, що значення функції
як функцію часу. Ймовірність того, що значення функції 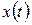 потрапляють в інтервал від
потрапляють в інтервал від 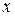 до
до 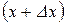 , можна знайти, обчислюючи відношення
, можна знайти, обчислюючи відношення 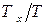 , де
, де 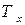 - сумарна тривалість знаходження значень реалізації
- сумарна тривалість знаходження значень реалізації 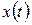 в інтервалі
в інтервалі 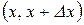 , за час спостереження. При прямуванні
, за час спостереження. При прямуванні  до нескінченості це відношення все точніше описує ймовірність такої події. Це твердження
до нескінченості це відношення все точніше описує ймовірність такої події. Це твердження

|
Рис. 3.4
можна записати наступним чином
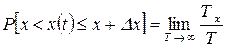 . (3.19)
. (3.19)
ОЗНАЧЕННЯ 3.11. Одновимірною щільністю розподілу ймовірностей називається функція 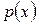 , яка при малих значеннях
, яка при малих значеннях  визначається співвідношенням
визначається співвідношенням
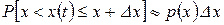 , (3.20)
, (3.20)
або більш строго
 . (3.21)
. (3.21)
Щільність розподілу 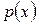 є завжди дійсною невід’ємною функцією.
є завжди дійсною невід’ємною функцією.
ОЗНАЧЕННЯ 3.12. Функція  , яка характеризує ймовірність того що миттєве значення процесу
, яка характеризує ймовірність того що миттєве значення процесу 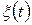 не перевищує деякої величини
не перевищує деякої величини 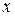 , називається функцією розподілу ймовірності цього процесу, тобто
, називається функцією розподілу ймовірності цього процесу, тобто
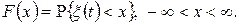 (3.22)
(3.22)
Функція розподілу  зв’язана із щільністю розподілу випадкового процесу наступним аналітичним співвідношенням
зв’язана із щільністю розподілу випадкового процесу наступним аналітичним співвідношенням
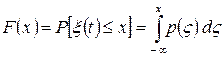 , (3.23)
, (3.23)
Функція розподілу  обмежена значеннями нуль і одиниця, оскільки ймовірність того, що
обмежена значеннями нуль і одиниця, оскільки ймовірність того, що 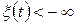 , вочевидь, дорівнює нулю, а ймовірність того, що
, вочевидь, дорівнює нулю, а ймовірність того, що  , дорівнює одиниці (достовірна подія). Ймовірність попадання
, дорівнює одиниці (достовірна подія). Ймовірність попадання 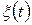 у деякий інтервал
у деякий інтервал 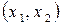 складає
складає
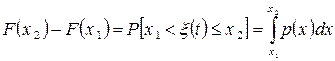 . (3.24)
. (3.24)
Середнє значення функції 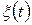 виражається через щільність розподілу наступним чином
виражається через щільність розподілу наступним чином
 , (3.25)
, (3.25)
тобто, середнє значення рівне зваженій сумі всіх значень процесу 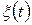 .
.
Аналогічно дисперсія процесу 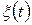
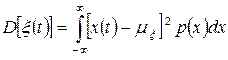 . (3.26)
. (3.26)
Іноді  називають інтегральною функцією розподілу, а
називають інтегральною функцією розподілу, а 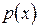 - диференціальною функцією розподілу.
- диференціальною функцією розподілу.
Значення функції 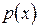 не є ймовірностями якихось подуй (це щільність) i можуть бути більшими, ніж 1. Вони мають розмірність, обернену розмірності, що відноситься до значень самої випадкової величини.
не є ймовірностями якихось подуй (це щільність) i можуть бути більшими, ніж 1. Вони мають розмірність, обернену розмірності, що відноситься до значень самої випадкової величини.
Характеристична функція випадкового процесу
ОЗНАЧЕННЯ 3.13. Характеристичною функцією випадкового процесу 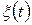 називається математичне сподівання випадкової функції
називається математичне сподівання випадкової функції 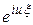 , тобто:
, тобто:
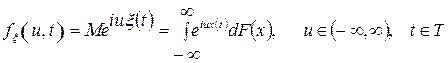 , (3.27)
, (3.27)
де 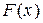 - функція розподілу випадкового процесу
- функція розподілу випадкового процесу 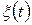 .
.
ЗАУВАЖЕННЯ. Символ  для
для  , як і
, як і 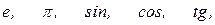 - ввів в 1777 році Л.Ейлер.
- ввів в 1777 році Л.Ейлер.
Для неперервного випадкового процесу (3.27) набуває вигляд
 (3.28)
(3.28)
де 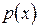 - щільність розподілу процесу
- щільність розподілу процесу 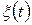 , а для дискретного
, а для дискретного
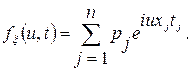 (3.29)
(3.29)
Якщо в 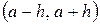 -
-  - околі точки
- околі точки  , функція
, функція 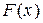 неперервна, за виключенням, можливо, самої точки
неперервна, за виключенням, можливо, самої точки 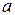 , то має місце обернене до (3.27) перетворення Фур'є-Стілтьєса:
, то має місце обернене до (3.27) перетворення Фур'є-Стілтьєса:
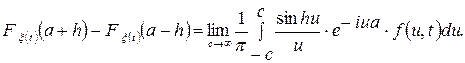 (3.30)
(3.30)
Якщо 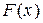 - нормована (тобто її значення в точці розриву приймається рівним
- нормована (тобто її значення в точці розриву приймається рівним 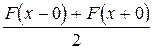 , то (3.30) справедливо для всіх
, то (3.30) справедливо для всіх 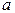 . Якщо в точці
. Якщо в точці 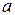 існує похідна
існує похідна 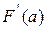 , то розділивши (3.30) на
, то розділивши (3.30) на 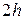 і перейшовши до границі при
і перейшовши до границі при 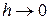 , отримаємо
, отримаємо
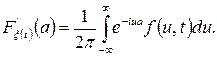 (3.31)
(3.31)
У випадку, коли існує 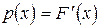 при всіх
при всіх 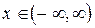 , то приймаючи до уваги (3.31), для (3.28) отримаємо обернене перетворення Фур'є
, то приймаючи до уваги (3.31), для (3.28) отримаємо обернене перетворення Фур'є
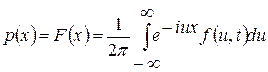 . (3.32)
. (3.32)
Слід зазначити, що завдання характеристичної функції в комплексній площині дещо ускладнює її практичне застосування для опису випадкового процесу 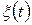 . Однак той факт, що ця функція завжди існує і повністю досліджуваний випадковий процес, робить її незамінною при глибокому аналізі багатьох класів випадкових процесів. Особливо це стосується такого важливого класу, як випадкові процеси с безмежно – подільними законами розподілу. Для цих процесів існують три форми канонічного представлення характеристичної функції, які забезпечують, так зване, конструктивне завдання досліджуваного процесу, що надає можливість докладно проаналізувати властивості таких процесів з урахуванням їх структури (наприклад, неперервної та імпульсної складових).
. Однак той факт, що ця функція завжди існує і повністю досліджуваний випадковий процес, робить її незамінною при глибокому аналізі багатьох класів випадкових процесів. Особливо це стосується такого важливого класу, як випадкові процеси с безмежно – подільними законами розподілу. Для цих процесів існують три форми канонічного представлення характеристичної функції, які забезпечують, так зване, конструктивне завдання досліджуваного процесу, що надає можливість докладно проаналізувати властивості таких процесів з урахуванням їх структури (наприклад, неперервної та імпульсної складових).
Контрольні запитання
1. Дати означення фізичних і математичних моделей.
2. В залежності від постановки задачі досліджень використовуються різні моделі сигналів: фізичні, математичні. Що в таких моделях сигналів спільного і чим вони відрізняються?
3. Навести означення випадкового процесу і його реалізації.
4. Як задати випадковий процес? В якій мірі описує цей процес його скінченновимірна послідовність функцій розподілу, які основні властивості такої послідовності?
5. Навести узагальнену класифікацію випадкових процесів, базуючись як на характерних властивостях самих процесів так і на характеристиках цих процесів.
6. Які випадкові процеси називаються стаціонарними?
7. Записати аналітичні вирази для математичного сподівання і кореляційної функції стаціонарного випадкового процесу.
8. Дати означення ергодичного випадкового процесу.
9. Яка основна особливість математичного сподівання та автокореляційної функції ергодичного випадкового процесу?
10. Які задачі розв’язуються в рамках кореляційної (енергетичної) теорії випадкових процесів.
11. Навести основні числові і функціональні характеристики випадкових процесів.
12. Записати аналітичні вирази для математичного сподівання і дисперсії випадкового процесу.
13. Привести означення коваріаційної функції випадкового процесу.
14. Навести означення для кореляційної функції випадкового процесу.
15. Записати аналітичний вираз, що характеризує зв’язок між коваріаційною і кореляційною функцією випадкового процесу.
16. Що характеризують коваріаційна і кореляційна функції у дійсному випадковому процесі?
17. Пояснити практичне застосування кореляційної функції при дослідженні дійсного випадкового процесу.
18. Навести означення спектральної щільності потужності випадкового процесу.
19. Дати визначення щільності розподілу випадкового процесу.
20. Навести означення та властивості функції розподілу  випадкового процесу.
випадкового процесу.
21. Привести означення та властивості щільності розподілу ймовірностей 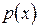 випадкового процесу
випадкового процесу 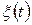 .
.
22. Як визначити функцію розподілу  , якщо задана щільність розподілу ймовірностей
, якщо задана щільність розподілу ймовірностей 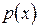 ?
?
23. Дати означення характеристичної функції випадкового процесу.
24. Як пов’язані між собою функція, щільність та характеристична функції розподілу ймовірностей випадкового процесу?